Text Book Solutions to Applications of Matrices and Determinants

Dear Students, here are the answers for the book back exercises in Business Maths Solutions for Chapter 1 Applications of Matrices and Determinants. If you have any doubts, please reach out to us in the comments section.

Click here if you want to revise:

Important Formulas in Chapter 1 Matrices and Determinants

Examples in Chapter 1 Matrices and Determinants

Text Book Solutions for Exercise 1.2

Text Book Solutions for Exercise 1.3

Text Book Solutions for Exercise 1.4

Text Book Solutions Exercise 1.1

$1. (i) Find \: the \:rank \:of \:the \:matrix \begin{pmatrix} 5 &6 \\ 7& 8 \end{pmatrix}\\$

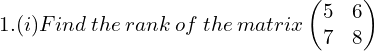
Order of A is 2 × 2

$\therefore \rho(A)\leq 2\\[.25 cm]$

Consider the second order minor

$\begin{vmatrix} 5 & 6\\ 7 & 8 \end{vmatrix}=40-42=-2\neq 0 \\[.25 cm]$

There is a minor of order 2, which is not zero. $\therefore \rho(A)= 2\\[.25 cm]$

$1. (ii) \: \begin{pmatrix} 1 &-1 \\ 3& -6 \end{pmatrix}\\[.25 cm]$

Order of A is 2 × 2

$\therefore \rho(A)\leq 2\\[.25 cm]$

Consider the second order minor

$\begin{vmatrix} 1 & -1\\ 3 & -6 \end{vmatrix} =-6- (-3) \\[.25 cm] =-6+3=-3 \neq 0 \\[.25 cm]$

There is a minor of order 2, which is not zero. $\therefore \rho(A)= 2\\[.25 cm]$

$1. (iii) \:\begin{pmatrix} 1 &4 \\ 2& 8 \end{pmatrix}\\[.25 cm]$

Order of A is 2 × 2

$\therefore \rho(A)\leq 2\\[.25 cm]$

Consider the second order minor

$\begin{vmatrix} 1 & 4\\ 2 & 8 \end{vmatrix} =0 \\[.25 cm]$

Consider a first order minor $\left | 1 \right |\neq 0 \\[.25 cm]$

There is a minor of order 1, which is not zero. $\therefore \rho(A)= 1\\[.25 cm]$

$1.(iv) \: \begin{bmatrix} 2 & -1 & 1 \\ 3 & 1 & -5 \\ 1 & 1 & 1 \end{bmatrix}\\[.25 cm]$

Order of A is 3 × 3

$\therefore \rho(A)\leq 3\\[.25 cm]$

Consider the third order minor

$= 2(1 + 5) - (-1) (3 + 5) + 1 (3 - 1)\\[.25 cm] = 2 (6) + 1(8) + 1(2) \\[.25 cm] = 12 + 8 + 2 \\[.25 cm] =22 \neq 0 \\[.25 cm]$

There is a minor of order 3, which is not zero. $\therefore \rho(A)= 3\\[.25 cm]$

$1. (v) \: \begin{bmatrix} -1 & 2 & -2 \\ 4 & -3 & 4 \\ -2 & 4 & -4 \end{bmatrix}\\[.25 cm]$

Order of A is 3 × 3

$\therefore \rho(A)\leq 3\\[.25 cm]$

Consider the third order minor $\begin{bmatrix} -1 & 2 & -2 \\ 4 & -3 & 4 \\ -2 & 4 & -4 \end{bmatrix}\\[.25 cm]$

$=-1(12 - 16) - 2 (-16 + 8) - 2 (16 - 6)\\[.25 cm] = -1(-4) - 2 (-8) - 2 (10) \\[.25 cm] = 4 + 16 - 20 \\[.25 cm] = 0 \\[.25 cm]$

Since the third order minor vanishes, $\therefore \rho(A) \neq 3\\[.25 cm]$

Consider a second order minor $\begin{vmatrix} -1 & 2\\ 4 & -3 \end{vmatrix} =3-8=-5 \neq 0 \\[.25 cm]$

There is a minor of order 2, which is not zero. $\therefore \rho(A)= 2\\[.25 cm]$

$1. (vi) \: \begin{bmatrix} 1 & 2 & -1 & 3 \\ 2 & 4 & 1 & -2 \\ 3 & 6 & 3 & -7 \end{bmatrix} \\[.25 cm]$

Order of A is 3 × 4

$\therefore \rho(A)\leq 3\\[.25 cm]$

A= \begin{bmatrix}1 & 2 & -1 & 3 \\2 & 4 & 1 & -2 \\3 & 6 & 3 & -7\end{bmatrix} \\[.25 cm]

The above matrix is in echelon form. The number of non zero rows is 2.

$\therefore \rho(A)=2\\[.5 cm]$

1. (vii) $\begin{bmatrix} 3 & 1 & -5 & -1 \\ 1 & -2 & 1 & -5 \\ 1 & 5 & -7 & 2 \end{bmatrix} \\[.25 cm]$

Order of A is 3 × 4

$\therefore \rho(A)\leq 3\\[.25 cm]$

Consider the third order minors $\begin{bmatrix} 3 & 1 & -5 \\ 1 & -2 & 1 \\ 1 & 5 & -7 \end{bmatrix} \\[.25 cm]$

$= 3 (14 - 5) - 1 (- 7 - 1) - 5 (5 + 2)\\[.25 cm] = 3 (9) - 1 (-8) - 5 (7)\\[.25 cm] = 27 + 8 - 35\\[.25 cm] = 0 \\[.25 cm]$

Consider the third order minors $\begin{bmatrix} 1 & -5 & 1 \\ -2 & 1 & -5 \\ 5 & -7 & 2 \end{bmatrix} \\[.25 cm]$

$= 1 (2-35) + 5 (-4 + 25) - 1 (14 - 5)\\[.25 cm] = 1(-33)+5(21)-1(9)\\[.25 cm] = -33+105-9\\[.25 cm] = 63 \neq 0 \\[.25 cm]$

There is a minor of order 3, which is not zero. $\therefore \rho(A)= 3\\[.5 cm]$

1. (viii) $\begin{bmatrix} 1 & -2 & 3 & 4 \\ -2 & 4 & -1 & -3 \\ -1 & 2 & 7 & 6 \end{bmatrix} \\[.25 cm]$

Order of A is 3 × 4

$\therefore \rho(A)\leq 3\\[.25 cm]$

A = \begin{bmatrix}1 & -2 & 3 & 4 \\-2 & 4 & -1 & -3 \\-1 & 2 & 7 & 6\end{bmatrix} \\[.25 cm]

A = \begin{bmatrix}1 & -2 & 3 & 4 \\0 & 0 & 5 & 5 \\0 & 0 & 10 & 10\end{bmatrix} \\[.25 cm]

The above matrix is in echelon form. The number of non zero rows is 2.

$2. \:If \: A =\: \begin{bmatrix} 1 & 1 & -1 \\ 2 & -3 & 4 \\ 3 & -2 & 3 \end{bmatrix} \: and \: B= \begin{bmatrix} 1 & -2 & 3 \\ -2 & 4 & -6 \\ 5 & 1 & -1 \end{bmatrix} \: then \: find \: the \: rank \: of \: AB \: and \: the \: rank \: of \: BA. \\[.25 cm]$

$AB = \begin{bmatrix} 1 & 1 & -1 \\ 2 & -3 & 4 \\ 3 & -2 & 3 \end{bmatrix} \begin{bmatrix} 1 & -2 & 3 \\ -2 & 4 & -6 \\ 5 & 1 & -1 \end{bmatrix}\\[.25 cm]$

$= \begin{bmatrix} 1-2-5 & -2+4-1 & 3-6+1 \\ 2+6+20 & -4-12+4 & 6+18-4 \\ 3+4+15 & -6-8+3 & 9+12-3 \end{bmatrix} \\[.25 cm]$

$AB = \begin{bmatrix} -6 & 1 & -2 \\ 28 & -12 & 20 \\ 22 & -11 & 18 \end{bmatrix} \\[.25 cm]$

$BA = \begin{bmatrix} 1 & -2 & 3 \\ -2 & 4 & -6 \\ 5 & 1 & -1 \end{bmatrix} \begin{bmatrix} 1 & 1 & -1 \\ 2 & -3 & 4 \\ 3 & -2 & 3 \end{bmatrix} \\[.25 cm]$

$= \begin{bmatrix} 1-4+9 & -1+6-6 & -1-8+9 \\ -2+8-18 & -2-12+12 & 2+16-18 \\ 5+2-3 & 5-3+2 & -5+4-3 \end{bmatrix} \\[.25 cm]$

$BA = \begin{bmatrix} 6 & 1 & 0 \\ -12& -2 & 0 \\ 4& 4& -4 \end{bmatrix} \\[.25 cm]$

Rank of AB:

Order of AB =3 x 3

Order of $\therefore \rho(A)\leq 3\\[.25 cm]$

Consider the third order minor, $AB = \begin{bmatrix} -6 & 1 & -2 \\ 28 & -12 & 20 \\ 22 & -11 & 18 \end{bmatrix} \\[.25 cm]$

$= -6(-216 + 220) -1(504 - 440) - 2(-308 + 264)\\[.25 cm] = - 6(4) - 1(64) - 2(-44)\\[.25 cm] = -24 - 64+ 88\\[.25 cm] = 0 \\[.25 cm]$

Since the third order minor vanishes, we consider the 2nd order minor.

$\large \begin{vmatrix} 1 & -2\\ -12 & 20 \end{vmatrix}=20-24\\[.25 cm] =-4 \neq 0 \\[.25 cm]$

There is a minor of order 2, which is not zero. $\therefore \rho(A)= 2\\[.25 cm]$

Rank of BA:

order of BA = 3 x 3

Order of $\therefore \rho(A)\leq 3\\[.25 cm]$

Consider the third order minor, $BA = \begin{bmatrix} 6 & 1 & 0 \\ -12& -2 & 0 \\ 4& 4& -4 \end{bmatrix} \\[.25 cm]$

$= 6(8 - 0) - 1(48 - 0) + 0(-48 + 8)\\[.25 cm] = 6(8) - 1(48) + 0(-40)\\[.25 cm] = 48 - 48 + 0 \\[.25 cm] = 0 \\[.25 cm]$

Since the third order minor vanishes, $\rho(A)\neq 3\\[.25 cm]$

Now, let us consider the second order minors,

Consider a second order minor $\large \begin{vmatrix} -12 & -2\\ 4 & 4 \end{vmatrix}=-48+8\\[.25 cm] =-40 \neq 0 \\[.25 cm]$

There is a minor of order 2, which is not zero. $\therefore \rho(A)= 2\\[.25 cm]$

3. Solve the following system of equations by rank method: x + y + z = 9, 2x + 5y + 7z = 52, 2x − y −z= 0

The matrix equation is $\begin{bmatrix} 1 & 1 & 1 \\ 2 & 5 & 7 \\ 2 & -1 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 9 \\ 52 \\ 0 \end{bmatrix} \\[.25 cm]$

\begin{bmatrix}1 & 1 & 1 & 9 \\2 & 5 & 7 & 52 \\2 & -1 & -1 & 0\end{bmatrix}\\[.25 cm]

The matrix is in the echelon form with three non-zero rows.
$\rho(A)=3 \: \rho([A,B]) =3 \\[.25 cm]$

Therefore, the given system is consistent and has a unique solution.

$\begin{bmatrix} 1 & 1 & 1 \\ 0 & 3 & 5 \\ 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} \begin{bmatrix} 9 \\ 34 \\ 16 \end{bmatrix} \\[.25cm]$

$x + y + z = 9\cdots (1)\\[.25 cm] 3y + 5z = 34 \cdots (2)\\[.25 cm] 2z = 16 \cdots (3)\\[.25 cm] z = 8 \\[.25 cm] Substitute \: z = 8 \: in \cdots (2) \\[.25 cm] 3y + 5 (8) = 34 \\[.25 cm] 3y + 40 = 34 \\[.25 cm] 3y = 34 - 40 \\[.25 cm] 3y = -6 \\[.25 cm] y = -2 \\[.25 cm] Substitute \: y = -2 \: and \: z = 8 \: in \cdots (1) \\[.25 cm] x = (-2) + 8 = 9 \\[.25 cm] x + 6 = 9 \\[.25 cm] x = 9 - 6 \\[.25 cm] x = 3 \\[.25 cm] \therefore x = 3, y = -2, z = 8 \\[.25cm]$

4. Show that the equations 5x + 3y + 7z = 4, 3x + 26y + 2z = 9, 7x + 2y + 10z = 5 are consistent and solve them by rank method.
Solution:
5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5

The matrix equation is $\begin{bmatrix} 5 & 3 & 7 \\ 3 & 26 & 2 \\ 7 & 2 & 10 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 4 \\ 9 \\ 5 \end{bmatrix} \\[.25 cm]$

\begin{bmatrix}5 & 3 & 7 & 4 \\0& 121& -11 & 33 \\0 & -11 & 1 & -3\end{bmatrix}\\[.25 cm]

The matrix is in the echelon form with two non-zero rows.

$\rho(A)= \rho([A,B]) =2=n \\[.25 cm]$

The matrix equation is $\begin{bmatrix} 5 & 3 & 7 \\ 0 & 121& -11 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 4 \\ 33 \\ 0 \end{bmatrix} \\[.25 cm]$

$5x + 3y + 7z = 4\cdots (1)\\[.25 cm] 121y -11z = 33 \cdots (2)\\[.25 cm] Put \: z = k \cdots (3)\\[.25 cm] Substitute \: z = k \: in \cdots (2) \\[.25 cm] 121y -11k = 33 \cdots \: divide \: by \: 11 \\[.25 cm] 11y -k = 3 \\[.25 cm] 11y = 3 + k \\[.25 cm] y=\frac{3+k}{11} \\[.5 cm] 5x+3(\frac{3+k}{11})+7k=4 \\[.5 cm] 5x+(\frac{9+3k}{11})+7k=4 \\[.5 cm] 5x+(\frac{9+3k+77k}{11})=4 \\[.5 cm] 5x+(\frac{9+80k}{11})=4 \\[.5 cm] 5x = 4 -(\frac{9+80k}{11})\\[.5 cm] 5x=(\frac{44-9-80k}{11})\\[.5 cm] 5x=(\frac{35-80k}{11})\\[.5 cm] 5x=5(\frac{7-16k}{11})\\[.5 cm] x=(\frac{7-16k}{11})\\[.5 cm] \therefore x=\frac{7-16k}{11}; \: y=\frac{3+k}{11}; \: z=k \:where \: k \in R \\[.25cm]$

5. Show that the following system of equations have unique solutions: x + y + z = 3, x + 2y + 3z = 4, x + 4y + 9z = 6 by rank method.

The matrix equation is $\begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 4 & 9 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 3 \\ 4 \\ 6 \end{bmatrix} \\[.25 cm]$

\begin{bmatrix}1 & 1 & 1 & 3 \\1& 2& 3& 4 \\1 & 4 & 9 & 6\end{bmatrix}\\[.25 cm]

The matrix is in the echelon form with three non-zero rows.

$\rho(A) \: \rho([A,B]) =3 = n \\[.25 cm]$

Therefore, the given system is consistent and a unique solution.

6. For what values of the parameter λ, will the following equations fail to have unique solution:
3x – y + λz = 1, 2x + y + z = 2, x + 2y – λz = -1.

The matrix equation is $\begin{bmatrix} 3 & -1 & \lambda \\ 2 & 1 & 1 \\ 1 & 2 & -\lambda \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 1 \\ 2 \\ -1 \end{bmatrix} \\[.25 cm]$

\begin{bmatrix}3 & -1 & \lambda & 1 \\2 & 1 & 1& 2 \\1 & 2 & -\lambda & -1\end{bmatrix}\\

$Since \: the\: equations\: fail\: to\: have\: a \:unique \:solution, \: \rho (A) \neq \:\rho ([A,B]) \\$

$\rho (A) \neq 3 \:\rho ([A,B]) =3 \\$

$\therefore 7 + 2\lambda = 0 \\$
$2\lambda = -7 and \lambda = -7/2\\$

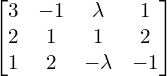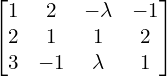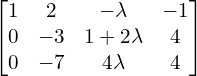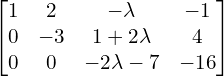7. The price of three commodities. X, Y, and Z are x,y, and z respectively Mr. Anand purchases 6 units of Z and sells 2 units of Y. Mr. Amar purchases a unit of Y and sells 3 units of X and 2 units of Z. Mr. Amit purchases a unit of X and sells 3 units of Y and a unit of Z. In the process they earn Rs 5,000/-, Rs 2,000/- and Rs 5,500/- respectively. Find the prices per unit of three commodities by the rank method.

Let the equations be:
2x + 3y – 6z = 5000
3x – y + 2z = 2000
-x + 3y + z = 5500

The matrix equation is $\begin{bmatrix} 2 & 3 & -6 \\ 3 & -1 & 2 \\ -1 & 3 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 5000\\ 2000 \\ 5500 \end{bmatrix} \\[.25 cm]$

\begin{bmatrix}2 & 3 & -6 & 5000 \\3 & -1 & 2 & 2000 \\-1 & 3 & 1 & 5500\end{bmatrix}\\[.25 cm]

The given system is consistent and has a unique solution.

The matrix equation is $\begin{bmatrix} -1 & 4 & -8 \\ 0 & 1 & -2 \\ 0 & 0 & 7 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 3000\\ 1000 \\ 3500 \end{bmatrix} \\[.25 cm]$

$-x + 4y - 8z =3000 \cdots (1)\\[.25 cm] y - 2 z = 1000 \cdots (2)\\[.25 cm] 7z = 3500 \cdots (3)\\[.25 cm] z=500 \\[.25 cm] Substituting \: z = 500 \: in \:Eq (2) \\[.25 cm] y - 2 (500) = 1000 \\[.25 cm] y - 1000 = 1000 \\[.25 cm] y = 2000 \\[.25 cm] Substituting \: z=500 \: and \: y = 2000 \: in \: Eq (1) \\[.25 cm] -x + 4 (2000) - 8 (500) = 3000 \\[.25 cm] -x + 8000 - 4000 = 3000 \\[.25 cm] - x = 3000 - 4000 \\[.25 cm] x = 1000 \\[.25 cm] \therefore the \: price \: of \: the \: three \: commodities \: are \: x= 1000, \:y=2000; \: z=500 \\[.25cm]$

8. An amount of Rs 5,000/- is to be deposited in three different bonds bearing 6%, 7%, and 8% per year respectively. Total annual income is Rs 358/-, If the income from the first two investments is Rs 70/- more than the income from the third, then find the amount of investment in each bond by the rank method.

Let the three bonds be x, y, and z.

$x + y + z = 5000 \cdots (1)\\$
$x (\frac{6}{100})$ + $y (\frac{7}{100})$ + $z (\frac{8}{100})$ = $358$

$\frac{6x}{100}$ + $\frac{7y}{100}$ + $\frac{8z}{100}$ = $358$

$6x +7y + 8z =35800 \cdots (2)$

$x (\frac{6}{100})$ + $y (\frac{7}{100})$ $= z(\frac{8}{100})$ + $70$

$\frac{6x}{100}$ + $\frac{7y}{100}$ = $\frac{8z}{100}$ + $70$

$6x + 7y = 8z + 7000 \\ 6x + 7y - 8z = 7000 \cdots (3)\\$

The matrix equation is $\begin{bmatrix} 1 & 1 & 1 \\ 6 & 7 & 8 \\ 6 & 7 & -8 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 5000\\ 35800 \\ 7000 \end{bmatrix} \\[.25 cm]$

\begin{bmatrix}1 & 1 & 1 & 5000 \\6 & 7 & 8 & 35800 \\6 & 7 & -8 & 7000\end{bmatrix}\\

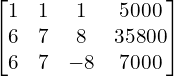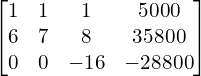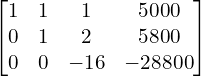The given system is consistent and has a unique solution.

The matrix equation is $\begin{bmatrix} 1 & 1 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & -16 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}= \begin{bmatrix} 5000\\ 5800 \\ -28800 \end{bmatrix} \\[.25 cm]$

$x + y + z = 5000 \cdots (1) \\[.25cm] y + 2z = 5800 \cdots (2) \\[.25cm] -16z = -28800 \cdots (3) \\[.25cm] z = \frac{-28800}{-16} \\[.25cm] z = 1800 \\[.25cm] Substituting \: z = 1800 \: in \: eqn (2) \\[.25cm] y + 2(1800) = 5800 \\[.25cm] y + 3600 = 5800 \\[.25cm] y = 5800 - 3600 \\[.25cm] y = 2200 \\[.25cm] Substituting \: z = 1800 \: y = 2200 \: in \: eqn (1) \\[.25cm] x + 2200 + 1800 = 5000 \\[.25cm] x + 4000 = 5000 \\[.25cm] x = 5000 - 4000 \\[.25cm] x = 1000 \\[.25cm] \therefore the \: amount \: of \: investment \: in \: each \: bond\: is \: x= 1000, \:y=2200; \: z=1800 \\[.25cm]$

If you have any doubts or questions, please reach out to us in the comments section.

Matrix A	Elementary Transformation
$A= \begin{bmatrix}1 & 2 & -1 & 3 \\2 & 4 & 1 & -2 \\3 & 6 & 3 & -7\end{bmatrix} \\[.25 cm]$
$\sim$ $A= \begin{bmatrix}1 & 2 & -1 & 3 \\0 & 0 & 3 & -8 \\0 & 0 & 6 & -16\end{bmatrix} \\[.25 cm]$	$R_{2}\rightarrow R_{2}- 2R_{1}\\R_{3}\rightarrow R_{3}- 3R_{1}$
$\sim$ $A= \begin{bmatrix}1 & 2 & -1 & 3 \\0 & 0 & 3 & -8 \\0 & 0 & 0 & 0\end{bmatrix} \\[.25 cm]$	$R_{3}\rightarrow R_{3}- 2R_{2}$

Matrix	Elementary Transformation
$A = \begin{bmatrix}1 & -2 & 3 & 4 \\-2 & 4 & -1 & -3 \\-1 & 2 & 7 & 6\end{bmatrix} \\[.25 cm]$
$A = \begin{bmatrix}1 & -2 & 3 & 4 \\0 & 0 & 5 & 5 \\0 & 0 & 10 & 10\end{bmatrix} \\[.25 cm]$	$R_{2}\rightarrow R_{2}+ 2R_{1}$ $R_{3}\rightarrow R_{3}+ R_{1}$
$A = \begin{bmatrix}1 & -2 & 3 & 4 \\0 & 0 & 5 & 5 \\0 & 0 & 0 & 0\end{bmatrix} \\[.25 cm]$	$R_{3}\rightarrow R_{3}- 2R_{2}$

Augmented Matrix	Elementary Transformation
$\begin{bmatrix}1 & 1 & 1 & 9 \\2 & 5 & 7 & 52 \\2 & -1 & -1 & 0\end{bmatrix}\\[.25 cm]$	$R_{2}\rightarrow R_{2}- 2R_{1}$ $R_{3}\rightarrow R_{3}- 2R_{1}$
$\sim$ $\begin{bmatrix}1 & 1 & 1 & 9 \\0 & 3 & 5 & 34 \\0 & -3 & -3 & -18\end{bmatrix} \\[.25 cm]$	$R_{3}\rightarrow R_{3}+R_{2}$
$\rho(A)=3\\[.25 cm]$	$\rho([A,B]) =3\\[.25 cm]$

Augmented Matrix	Elementary Transformation
$\begin{bmatrix}5 & 3 & 7 & 4 \\0& 121& -11 & 33 \\0 & -11 & 1 & -3\end{bmatrix}\\[.25 cm]$	$R_{2}\rightarrow 5R_{2}-3R_{3}$ $R_{3}\rightarrow 5R_{3}-7R_{1}$
$\sim$ $\begin{bmatrix}5 & 3 & 7 & 4\\0& 121& -11 & 33 \\0 & 0 & 0 & 0\end{bmatrix} \\[.25 cm]$	$R_{3}\rightarrow 11R_{3}+R_{2}$
$\rho(A)=2\\[.25 cm]$	$\rho([A,B]) =2\\[.25 cm]$

Augmented Matrix	Elementary Transformation
$\begin{bmatrix}1 & 1 & 1 & 3 \\1& 2& 3& 4 \\1 & 4 & 9 & 6\end{bmatrix}\\[.25 cm]$	$R_{2}\rightarrow R_{2}-R_{1}$ $R_{3}\rightarrow R_{3}-R_{1}$
$\sim$ $\begin{bmatrix}1 & 1 & 1 & 3 \\0& 1& 2& 1 \\0 & 3 & 8 & 3\end{bmatrix} \\[.25 cm]$	$R_{3}\rightarrow 11R_{3}+R_{2}$
$\sim$ $\begin{bmatrix}1 & 1 & 1 & 3 \\0& 1& 2& 1 \\0 & 0 & 2 & 0\end{bmatrix} \\[.25 cm]$	$R_{3}\rightarrow R_{3}+R_{2}$
$\rho(A)=3\\[.25 cm]$	$\rho([A,B]) =3\\[.25 cm]$

12th Business Maths Text Book Solutions for Applications of Matrices and Determinants

Text Book Solutions Exercise 1.1

Related Posts:

Leave a Reply Cancel reply

Recent

Text Book Solutions Exercise 1.1

Related Posts:

Reader Interactions

Leave a Reply Cancel reply

Footer

Recent

Tags