Class 12 Samacheer Kalvi students, here are the solutions to Exercise 1.4 in Chapter 1 Applications of Matrices and Determinants. (Business Maths). You can find links to the other exercises also below.
Important Formulas in Chapter 1 Matrices and Determinants
Examples in Chapter 1 Matrices and Determinants
Text Book Solutions for Exercise 1.1
Text Book Solutions for Exercise 1.2
Text Book Solutions for Exercise 1.3
Text Book Solutions Exercise1.4
Choose the correct answer:
| 1. If A=(1 2 3), then the rank of | |
| a) 0 | b) 2 |
| c) 3 | d) 1 |
| 2. The rank of m n × matrix whose elements are unity is | |
| a) 0 | b) 1 |
| c) m | d) n |
3. If 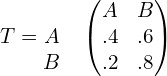 is a transition probability matrix, then at equilibrium A is equal to is a transition probability matrix, then at equilibrium A is equal to | |
| a) 1/4 | b) 1/5 |
| c) 1/6 | d) 1/8 |
4. If  | |
| a) 0 | b) 1 |
| c) 2 | d) n |
5. The rank of the matrix  is is | |
| a) 0 | b) 1 |
| c) 2 | d) 3 |
| 6. The rank of the unit matrix of order n is | |
| a) n-1 | b) n |
| c) n+1 | d) |
| 7. If | |
| (a) all the minors of order r which does not vanish | (b) A has at least one minor of order r which does not vanish |
| (c) A has at least one (r+1) order minor which vanishes | (d) all (r+1) and higher order minors should not vanish |
8. If  is is | |
| a) 0 | b) 1 |
| c) 2 | d) 3 |
9. If the rank of the matrix If 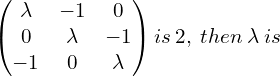 | |
| a) 1 | b) 2 |
| c) 3 | d) only real number |
10. The rank of the diagonal matrix  | |
| a) 0 | b) 2 |
| c) 3 | d) 5 |
11. If  is a transition probability matrix, then the value of x is is a transition probability matrix, then the value of x is | |
| a) 0.2 | b) 0.3 |
| c) 0.4 | d) 0.7 |
| 12. Which of the following is not an elementary transformation? | |
| a) | b) |
| c) | d) |
| 13. If | |
| a) Consistent and has infinitely many solutions | b) Consistent and has a unique solution |
| c) Consistent | d) inconsistent |
| 14. If | |
| a) Consistent and has infinitely many solutions | b) Consistent and has a unique solution |
| c) inconsistent | d) consistent |
| 15. If | |
| a) Consistent and has infinitely many solutions | b) Consistent and has a unique solution |
| c) inconsistent | d) consistent |
| 16. In a transition probability matrix, all the entries are greater than or equal to | |
| a) 2 | b) 1 |
| c) 0 | d) 3 |
| 17. If the number of variables in a non homogeneous system AX = B is n, then the system possesses a unique solution only when | |
| a) | b) |
| c) | d) none of these |
| 18. The system of equations 4x + 6y = 5, 6x + 9y = 7 has | |
| a) a unique solution | b) no solution |
| c) infinitely many solutions | d) none of these |
| 19. For the system of equations x +2y + 3z = 1, 2x +y + 3z = 2, 5x +5y + 9z = 4, | |
| a) there is only one solution | b) there exists infinitely many solutions |
| c) there is no solution | d) none of these |
| 20. If | |
| a) non- singular matrix | b) singular matrix |
| c) zero matrix | d) none of these |
| 21. The system of linear equations x + y + z = 2, 2x +y - z = 3, 3x +2y + k = 4, has unique solution, if k is not equal to | |
| a) 4 | b) 0 |
| c) -4 | d) 1 |
| 22. Cramer’s rule is applicable only to get a unique solution when | |
| a) | b) |
| c) | d) |
| 23. If | |
 , ,  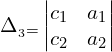 then (x,y) is then (x,y) is | |
| a) | b) |
| c) | d) |
| 24. | |
| a) 4 | b) 5 |
| c) 6 | d) 7 |
| 25. Rank of a null matrix is | |
| a) 0 | b) -1 |
| c) | d) 1 |
Leave a Reply