Differential Equations Exercise 4.1 Text Book Solutions

Dear Class 12 Samacheer Kalvi students, here are the Business Maths Chapter 4 Differential Equations Exercise 4.1 Text Book Solutions for your reference and study.

You can find links to the other exercises below.

Important Formulas and Notes in Differential Equations

Text Book Solutions for Differential Equations Exercise 4.2

Text Book Solutions for Differential Equations Exercise 4.3

Text Book Solutions for Differential Equations Exercise 4.4

Text Book Solutions for Differential Equations Exercise 4.5

Text Book Solutions for Differential Equations Exercise 4.6

Exercise 4.1

1. Find the order and degree of the following differential equations.

$(i)\dfrac{dy}{dx}+2y=x^{3}\\$
$Answer: \; Order=1; \; Degree=1\\$

$(ii)\dfrac{d^{3}y}{dx^{3}}+3 \left( \dfrac{dy}{dx} \right)^{3}+2 \dfrac{dy}{dx}=0\\$
$Answer: \; Order=3; \; Degree=1\\$

$(iii)\dfrac{d^{2}y}{dx^{2}}=\sqrt{y-\dfrac{dy}{dx}}\\$
$Squaring\; on \;both \;sides \\$
$\left( \dfrac{d^{2}y}{dx^{2}} \right)^{2}={y-\dfrac{dy}{dx}}\\$
$Answer: \; Order=2; \; Degree=2\\$

$(iv)\dfrac{d^{3}y}{dx^{3}}=0\\$
$Answer: \; Order=3; \; Degree=1\\$

$(v)\dfrac{d^{2}y}{dx^{2}}+y+\left( \dfrac{dy}{dx}-\dfrac{d^{3}y}{dx^{3}} \right)^{\frac{3}{2}}=0\\$
$\dfrac{d^{2}y}{dx^{2}}+y =- \left( \dfrac{dy}{dx}-\dfrac{d^{3}y}{dx^{3}} \right)^{\frac{3}{2}}\\$
$Squaring\; on \;both \;sides \\$
$\left( \dfrac{d^{2}y}{dx^{2}}+y \right)^{2} =- \left( \dfrac{dy}{dx}-\dfrac{d^{3}y}{dx^{3}} \right)^{3}\\$
$Answer: \; Order=3; \; Degree=3\\$

$(vi)(2-y'')^{2}=(y'')^{2}+2y'\\$
$4-4y''+(y'')^{2}+=(y'')^{2}+2y'\\$
$4-4y''=2y'\\$
$Answer: \; Order=2; \; Degree=1\\$

$(vii)\left( \dfrac{dy}{dx} \right)^{3}+y=x-\dfrac{dx}{dy}\\$
$Multiply \; by \; \dfrac{dy}{dx}\\$
$\left( \dfrac{dy}{dx} \right)^{3} \dfrac{dy}{dx}+y\dfrac{dy}{dx} =x \dfrac{dy}{dx}-1 \\$
$\left( \dfrac{dy}{dx} \right)^{4} +y\dfrac{dy}{dx} =x \dfrac{dy}{dx}-1 \\$
$Answer: \; Order=1; \; Degree=4\\$

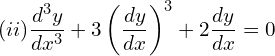
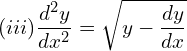
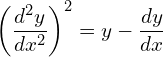
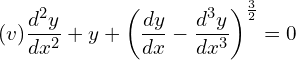
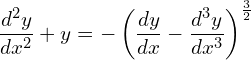
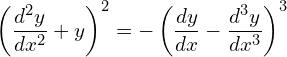
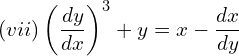
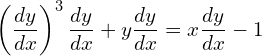
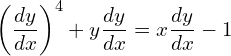
2. Find the differential equation of the following.

$(i)y=cx+c+c^{3}\\$
$Differentiate\; w.\; r.\; t. \; x\\$
$y'=c+0-0\\$
$y'=c\\$
$y=y'x+y'-(y')^{3}\\$
$y=x\dfrac{dy}{dx}+\dfrac{dy}{dx}-\left( \dfrac{dy}{dx} \right)^{3}$

$(ii)y=c(x-c)^{2}\cdots (1)\\$
$Differentiate\; w.\; r.\; t. \; x\\$
$y'=2c(x-c)\cdots (1)\\$
$Dividing \; \dfrac{(1)}{(2)}\\$
$\dfrac{y}{y'}=\dfrac{c(x-c)^{2}}{2c(x-c)}\\$
$\dfrac{y}{y'}=\dfrac{x-c}{2}\\$
$\dfrac{2y}{y'}=x-c\\$
$c= x- \dfrac{2y}{y'}\\$
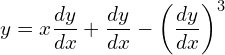
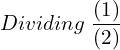
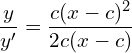
$(1)\\ y= \left( x-\dfrac{2y}{y'} \right) \left[ x- \left( x-\dfrac{2y}{y'} \right) \right] ^{2}\\$
$y= \dfrac{xy'-2y}{y'} \left( x-x+\dfrac{2y}{y'} \right)^{2}\\$
$y= \dfrac{xy'-2y}{y'} \left(\dfrac{2y}{y'} \right)^{2}\\$
$y= \dfrac{xy'-2y}{y'} \left(\dfrac{4y^{2}}{y'^{2}} \right)\\$
$y= \dfrac{4y^{2}}{y'^{3}} \left({xy'-2y}\right)\\$
$1= \dfrac{4y}{y'^{3}} \left({xy'-2y}\right)\\$
$y'^{3}= 4y \left({xy'-2y}\right)\\$
$y'^{3}= 4xyy'-8y^{2}\\$
$\left( \dfrac{dy}{dx} \right)^{3}-4xy\dfrac{dy}{dx}+8y^{2}=0\\$

$(iii)xy=c^{2} \\$
$Differentiate\; w.\; r.\; t. \; x\\$
$1(y)+x\dfrac{dy}{dx}=0\\$
$y+x\dfrac{dy}{dx}=0\\$

$(iv)x^{2}+y^{2}=a^{2} \\$
$Differentiate\; w.\; r.\; t. \; x\\$
$2x+2y\dfrac{dy}{dx}=0\\$
$x+y\dfrac{dy}{dx}=0\\$

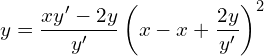
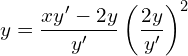
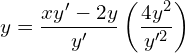
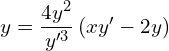
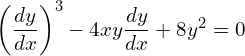
3. Form the differential equation by eliminating α and β from
$(x-\alpha)^{2}+(y-beta)^{2}=r^{2}$

$Let \; (x-\alpha)^{2}+(y-\beta)^{2}=r^{2}\cdots (1) \\$
$Differentiate\; w.\; r.\; t. \; x\\$
$Let \; 2(x-\alpha)+2(y-\beta)\dfrac{dy}{dx}=0$
$Let \; (x-\alpha)+(y-\beta)\dfrac{dy}{dx}=0 \cdots (2)\\$
$Differentiate\; w.\; r.\; t. \; x\\$
$1+(y'-0)y'+(y-\beta)y''=0 \\$
$1+y'^{2}+(y-\beta)y''=0 \\$
$(y-\beta)y''=-(1+y'^{2}) \\$
$(y-\beta)=\dfrac{-(1+y'^{2})}{y''}\\$
$(2)(x-\alpha)-\dfrac{(1+y'^{2})}{y''}\dfrac{dy}{dx}=0\\$
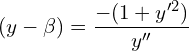
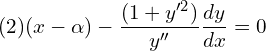
$(1) \left( \dfrac{(1+y'^{2})}{y''}y' \right)^{2}+ \left[ - \dfrac{(1+y'^{2})}{y''} \right]^{2}=r^{2}\\$
$\dfrac{(1+y'^{2})^{2}}{y''^{2}}y'^{2}+\dfrac{(1+y'^{2})^{2}}{y''^{2}}=r^{2}\\$
$\dfrac{(1+y'^{2})^{2}}{y''^{2}} (y'^{2}+1)=r^{2}\\$
$\dfrac{(1+y'^{2})^{3}}{y''^{2}} =r^{2}\\$
$(1+y'^{2})^{3} =r^{2}y''^{2}\\$
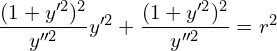
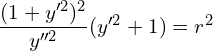
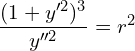
$r^{2}\left[ \dfrac{d^{2}y}{dx^{2}} \right]^{2} =\left[ 1+\left( \dfrac{dy}{dx} \right)^{2} \right]^{3}\\$

4. Find the differential equation of the family of all straight lines passing through the origin.

Answer: Equation of the family of all straight lines passing through the origin: y=mx

$y=mx \cdots (1) \\$
$Differentiate\; w.\; r.\; t. \; x\\$
$y'=m \\$
$y=y'x \cdots (1) \\$
$y=x \dfrac{dy}{dx}\cdots (1) \\$

5. Form the differential equation that represents all parabolas each of which has a latus rectum 4a and whose axes are parallel to the x axis.

$Let \; (y-k)^{2}=4a (x-h)$ be all parabolas each of which has a latus rectum 4a and whose axes are parallel to the x axis.

$(y-k)^{2}=4a (x-h)\\$
$Differentiate\; w.\; r.\; t. \; x\\$
$2(y-k)y'=4a (1-0)\\$
$2(y-k)y'=4a\\$
$(y-k)y'=2a\cdots (1)\\$
$Differentiate\; w.\; r.\; t. \; x\\$
$(y'-0)y'+(y-k)y'=0\\$
$y'^{2}+(y-k)y''=0\\$
$(y-k)y''=-y'^{2}\\$
$(y-k)=\dfrac{-y'^{2}}{y''}\\$
$(1)\left( \dfrac{-y'^{2}}{y''} \right)y'=2a\\$
$-y'^{3}=2ay''\\$
$0=2ay''+y'^{3}\\$
$2a\dfrac{d^{2}y}{dx^{2}}+\left( \dfrac{dy}{dx} \right)^{3}=0\\$

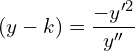
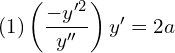
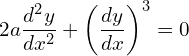
6. Find the differential equation of all circles passing through the origin and having their centers on the y axis.

$Center = (0,a) or(h,k)\\$
$radius = a \\$
$(x-h)^{2}+(y-k)^{2}=r^{2} \\$
$(x-0)^{2}+(y-a)^{2}=a^{2} \\$
$x^{2}+(y-a)^{2}=a^{2} \\$
This is the equation of the circle passing through the origin and having centre on the y axis.

$x^{2}+y^{2}-2ay+a^{2} =a^{2} \\$
$x^{2}+y^{2}-2ay=0 \Rightarrow (1) \\$
$Differentiating \; w.r.t\;x \\$
$2x+2yy'-2y'a=0 \\$
$Dividing \;by \;2 \\$
$x+yy'-y'a=0 \\$
$x+yy'=y'a \\$
$a=\frac{x+yy'}{y'} \\$
$a=\frac{x}{y'}+y \\$
$Substituting \; a \;in \;Eq (1) \\$
$x^{2}+y^{2}-2y\;(\left( \frac{x}{y'}+y \right)=0 \\$
$x^{2}+y^{2}-\frac{2xy}{y'}-2y^{2}=0 \\$
$x^{2}-y^{2}-\frac{2xy}{y'}=0 \\$
$x^{2}=y^{2}+\frac{2xy}{y'} \\$
$x^{2}=y^{2}+\frac{2xy}{\frac{dy }{dx}} \\$

7. Find the differential equation of the family of parabola with foci at the origin and axis along the x-axis.

$Let \; y^{2}=4a(x+a)$ be the family of parabola with foci at the origin and axis along the x-axis.
$y^{2}=4a(x+a) \Rightarrow (1) \\$
$Differentiating \; w.r.t\;x \\$
$2yy'=4a(1+0)) \\$
$2yy'=4a \\$
$yy'=2a \\$
$a=\frac{yy'}{2} \\$
Substituting a in Eq.1
$y^{2}=4\left( \frac{yy'}{2} \right)\left( x+\frac{yy'}{2} \right) \\$
$y^{2}=2yy'\left( \frac{2x+yy'}{2} \right) \\$
$y^{2}=yy'\left( 2x+yy'\right) \\$
$y=y'\left( 2x+yy'\right) \\$
$y=2xy'+yy'^{2} \\$
$y=2x\frac{dy}{dx}+y \left( \frac{dy}{dx} \right) ^{2} \\$