Important Formulas in Integral Calculus I

Dear students, before you start revision for the chapter Integral Calculus I, first make sure you revise all the formulas and key points. Only if you are thorough with the main concepts and formulas, you can confidently work out all the sums. That said, here are the most important formulas in Integral Calculus I, Class 12 Business Maths.

You can find links to the other exercises also below.

Text Book Solutions for Integral Calculus I Exercise 2.1

Text Book Solutions for Integral Calculus I Exercise 2.2

Text Book Solutions for Integral Calculus I Exercise 2.3

Text Book Solutions for Integral Calculus I Exercise 2.4

Text Book Solutions for Integral Calculus I Exercise 2.5

Text Book Solutions for Integral Calculus I Exercise 2.6

Text Book Solutions for Integral Calculus I Exercise 2.7

Text Book Solutions for Integral Calculus I Exercise 2.8

Text Book Solutions for Integral Calculus I Exercise 2.9

Text Book Solutions for Integral Calculus I Exercise 2.10

Text Book Solutions for Integral Calculus I Exercise 2.11

Text Book Solutions for Integral Calculus I Exercise 2.12 (MCQ)

Important Formulas and Notes in Integral Calculus I

Properties of indefinite integrals

$1. \int a f (x) dx = a \int f (x) dx \\$

$2. \int [f (x)\pm g (x)] dx =\int f (x) dx \pm \int g (x) dx \\$

Standard results of indefinite integrals

$1. \int x^{n} dx =\frac{x^{n+1}}{n+1}+c\\$

$2. \int \frac{1}{x} dx = log\left | x \right |+c\\$

$3. \int e^{x} dx = e^{x} +c\\$

$4.\int a^{x} dx = \dfrac{1}{log a}a^{x} +c \\$

$5.\int sin x dx = -cos x +c \\$

$6.\int cos x dx = sin x +c \\$

$7.\int sec^{2}x dx = tan x +c \\$

$8.\int cosec^{2}x dx = -cot x +c \\$

$9.\int cosec^{2}x dx = -cot x +c \\$

$9.\int [f(x)]^{n} f' (x) = \frac{[f(x)]^{n+1}}{n+1}+c \\$

$10.\int \frac{f'(x) }{f (x)}dx = log \left |f(x) \right |+c \\$

$11.\int \frac{f'(x)}{\sqrt{f(x)}}dx = 2\sqrt{f (x)}+c\\$

$12.\int udv = uv-\int vdu \\$

$13.\int udv = uv-u'v_{1}+u''v_{2}-u''' v_{3}+\cdots \\$

$14.\int \dfrac{dx}{a^{2}-x^{2}} = \dfrac{1}{2a}log \left | \dfrac{a+x}{a-x} \right |+c\\$

15. $\int \dfrac{dx}{x^{2}-a^{2}}dx = \dfrac{1}{2a}log \left | \dfrac{x-a}{x+a} \right |+c\\$

16. $\int \dfrac{dx}{\sqrt{x^{2}-a^{2}}} = log \left | x+\sqrt{x^{2}-a^{2}} \right |+c \\$

17. $\int \dfrac{dx}{\sqrt{x^{2}+a^{2}}} = log \left | x+\sqrt{x^{2}+a^{2}} \right |+c \\$

18. $\int e^{x}[f(x)+f'(x)] dx = e^{x}f(x)+c\\$

19. $\int e^{ax}[a f(x)+f'(x)] dx = e^{ax}f(x)+c\\$

20. $\int \sqrt{x^{2}-a^{2}} dx = \dfrac{x}{2}\sqrt{x^{2}-a^{2}}-\dfrac{a^{2}}{2}log \left |x+\sqrt{x^{2}-a^{2}} \right |+c\\$

21. $\int \sqrt{x^{2}+a^{2}} dx = \dfrac{x}{2}\sqrt{x^{2}+a^{2}}+\dfrac{a^{2}}{2}log \left |x+\sqrt{x^{2}+a^{2}} \right |+c\\$

Properties of definite integrals

$1. \int \limits_{a}^{b} f(x) dx =\int \limits_{a}^{b} f(t) dt\\$

$2. \int \limits_{a}^{b} f(x) dx =-\int \limits_{b}^{a} f(x) dx\\$

$3. \int \limits_{a}^{b} [f(x) \pm g (x)]dx = \int \limits_{a}^{b} f(x)dx \pm \int \limits_{a}^{b} g (x)dx\\$

$4. \int \limits_{a}^{b} f(x) dx = \int \limits_{a}^{c} f(x) dx + \int \limits_{c}^{b} f(x) dx \\$

$5. \int \limits_{0}^{a} f(x) dx =\int \limits_{0}^{a} f(a-x) dx\\$

$6. \int \limits_{a}^{b} f(x) dx =\int \limits_{a}^{b} f(a+b-x) dx\\$

$7. \: a) \: If \: f (x )\: is \: an \: even\: function, \: then \: \int \limits_{-a}^{a} f(x) dx = 2 \int \limits_{0}^{a} f(x) dx \\$
$\: b) \: If\: f(x)\: is\: an\: odd \: function, \: then\: \int \limits_{-a}^{a} f(x) dx =0 \\$

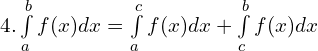
Particular case of Gamma Integral

$If \:n \: is \:a \:positive \:integer, \:then \:\int \limits_{0}^{\infty}x^{n}e^{ax} dx = \dfrac{n!}{a^{n-1}}\\$

Properties of gamma function

$1. \Gamma (n) =(n-1) \: \Gamma (n-1), \: n> 1\\$

$2. \Gamma (n+1) =n\: \Gamma (n), \: n> 0\\$

$3. \Gamma (n+1) = n!, \: n \: is \: a \: positive \: integer.\\$

$4. \Gamma (\frac{1}{2})=\sqrt{\pi}\\$

Definite integral as the limit of a sum

Let f ( x) be a continuous real valued function in $[a, b]$ , which is divided into n equal parts each of width h , then: $\int_{a}^{b} f(x) dx=\lim_{h\rightarrow 0 \: n\rightarrow \infty}\sum\limits_{r=1}^{n} h f(a+rh)$ where $h=\frac{b-a}{n}$

Some More Results

$1+2+3+\cdots \cdots n = \dfrac{n (n+1)}{2} =\sum\limits_{r=1}^{n}r\\$

$1^{2}+2^{2}+3^{2}+\cdots \cdots n^{2} = \dfrac{n (n+1)(2n+1)}{6} =\sum\limits_{r=1}^{r=n}r^{2}\\$

$1^{3}+2^{3}+3^{3}+\cdots \cdots n^{3} = \left [\dfrac{n(n+1)}{2} \right ]^{2} = \sum\limits_{r=1}^{r=n}r^{3}\\$

Important Formulas and Notes in Integral Calculus I

Important Formulas and Notes in Integral Calculus I

Properties of indefinite integrals

Standard results of indefinite integrals

Properties of definite integrals

Particular case of Gamma Integral

Properties of gamma function

Definite integral as the limit of a sum

Some More Results

Related Posts:

Leave a Reply Cancel reply

Recent

Important Formulas and Notes in Integral Calculus I

Properties of indefinite integrals

Standard results of indefinite integrals

Properties of definite integrals

Particular case of Gamma Integral

Properties of gamma function

Definite integral as the limit of a sum

Some More Results

Related Posts:

Reader Interactions

Leave a Reply Cancel reply

Footer

Recent

Tags