Integral Calculus I Exercise 2.8 - 12th Text Book Solutions

Dear Samacheer Kalvi Students, here are the answers for book back exercise 2.7 in Business Maths Chapter 2 Integral Calculus I. If you have any doubts, please reach out to us in the comments section.

Click here if you want to revise:

Important Formulas in Integral Calculus I

Text Book Solutions for Integral Calculus I Exercise 2.1

Text Book Solutions for Integral Calculus I Exercise 2.2

Text Book Solutions for Integral Calculus I Exercise 2.3

Text Book Solutions for Integral Calculus I Exercise 2.4

Text Book Solutions for Integral Calculus I Exercise 2.5

Text Book Solutions for Integral Calculus I Exercise 2.6

Text Book Solutions for Integral Calculus I Exercise 2.7

Text Book Solutions for Integral Calculus I Exercise 2.9

Text Book Solutions for Integral Calculus I Exercise 2.10

Text Book Solutions for Integral Calculus I Exercise 2.11

Text Book Solutions for Integral Calculus I Exercise 2.12 (MCQ)

Exercise 2.8

I. Using the second fundamental theorem, evaluate the following:

$1. \displaystyle \int_{0}^{1}e^{2x} \: dx$

$\displaystyle \int_{0}^{1}e^{2x} \: dx ={\left [\dfrac{e^{2x}}{2} \right ]_{0}}^{1}\\$
$=\dfrac{1}{2}{\left [{e^{2x}} \right ]_{0}}^{1}\\$
$=\dfrac{1}{2}\left [ e^{2(1)}-e^{2(0)} \right ]\\$
$=\dfrac{1}{2}\left ( e^{2}-1 \right )+c$

$2. \displaystyle \int_{0}^{\frac{1}{4}}\sqrt{1-4x}\: dx\\$

$= \displaystyle \int_{0}^{\frac{1}{4}}\left ({1-4x} \right )^{\frac{1}{2}}\: dx\\$
$= \displaystyle \int_{0}^{\dfrac{1}{4}}\left ({1-4x} \right )^{\frac{1}{2}}\: dx\\$
$= \left [\dfrac{\left (1-4x \right )^{\frac{1}{2}+1}}{(-4)\left ( \frac{1}{2}+1 \right )} \right ]_{0}^{\frac{1}{4}}\\$
$= \displaystyle \int_{0}^{\frac{1}{4}}\left ({1-4x} \right )^{\frac{1}{2}}\: dx\\$
$= \left [\dfrac{\left (1-4x \right )^{\frac{1}{2}+1}}{(-4)\left ( \frac{1}{2}+1 \right )} \right ]_{0}^{\frac{1}{4}}\\$
$= \left [\dfrac{\left (1-4x \right )^{\frac{3}{2}}}{(-4)\left ( \frac{3}{2} \right )} \right ]_{0}^{\frac{1}{4}}\\$
$= \left [\dfrac{\left (1-4x \right )^{\frac{3}{2}}}{(-6)} \right ]_{0}^{\frac{1}{4}}$
$=\dfrac{-1}{6}\left [ \left (1-4x \right )^{\frac{3}{2}}\right ]_{0}^{\frac{1}{4}}\\$
$=\dfrac{-1}{6}\left [\left ( 1-4 \times \frac{1}{4} \right )^{\frac{3}{2}}-\left (1-4(0) \right )^{\frac{3}{2}}\right ]+c\\$
$=\dfrac{-1}{6}\left ( 0-1 \right )\\$
$=\dfrac{1}{6}$

$3. \displaystyle \int_{1}^{2} \frac{x\: dx}{x^{2}+1}\\$

$I = \displaystyle \int_{1}^{2} \frac{x\: dx}{x^{2}+1}\\$
$Put\: t=x^{2}+1\\$
$dt=2x\: dx\\$
$\dfrac{dt}{2}=x \: dx\\$

$I=\displaystyle \int_{2}^{5} \dfrac{\frac{dt}{2}}{t}\\$
$=\dfrac{1}{2} \displaystyle \int \dfrac{dt}{t}\\$
$=\dfrac{1}{2} \bigg[ log \left | t \right |\bigg ] _{2}^{5}$
$=\dfrac{1}{2}\left ( log \: 5 -log \:2 \right )\\$
$=\dfrac{1}{2}\left (log \: \frac{5}{2} \right )$

$4. \displaystyle \int_{0}^{3} \frac{e^{x}dx}{1+e^{x}}$

$I = \displaystyle \int_{0}^{3} \frac{e^{x}dx}{1+e^{x}}\\$
$Put \: t=1+e^{x}\\$
$dt=e^{x}dx$

$I= \displaystyle \int_{2}^{1+e^{x}} \dfrac{dt}{t}\\$
$= \bigg [ log \left |t \right | \bigg ]_{2}^{1+e^{x}}$
$=log\left ( 1+e^{x} \right )-log\: 2$
$=log\left | \dfrac{1+e^{3}}{2} \right |$

$5. \displaystyle \int_{0}^{1} x\: e^{x^{2}}\: dx$

$I = \displaystyle \int_{0}^{1} x\: e^{x^{2}}\: dx\\$
$Put \: t=x^{2}\\$
$dt = 2x \: dx\\$
$\dfrac{dt}{2}= x \: dx\\$

$I = \displaystyle \int_{0}^{1} e^{t}\:\dfrac{ dt}{2}\\$
$= \dfrac{1}{2}\displaystyle \int_{0}^{1} e^{t}\: dt\\$
$=\dfrac{1}{2}\bigg[ e^{t} \bigg]_{0}^{1}\\$
$=\dfrac{1}{2} \left [ e^{1}-e^{0} \right ]\\$
$=\dfrac{1}{2} \left ( e-1 \right )$

$6. \displaystyle \int_{1}^{e} \dfrac{dx}{x\left ( 1+log x \right )^{3}}$

$I = \displaystyle \int_{1}^{e} \dfrac{dx}{x\left ( 1+log x \right )^{3}}\\$
$Put \: t=1+log x\\$
$dt=\dfrac{1}{x}\: dx\\$

$=\displaystyle \int_{1}^{2} \dfrac{dt}{ ( t)^{3}}\\$
$=\displaystyle \int_{1}^{2} { t^{-3}dt}\\$
$=\bigg[\dfrac{t^{-2}}{-2} \bigg ]_{1}^{2} \\$
$=\dfrac{-1}{2} \bigg[\dfrac{1}{t^{2}} \bigg]_{1}^{2}\\$
$=\dfrac{-1}{2} \bigg[\dfrac{1}{4} -1 \bigg]\\$
$=\dfrac{-1}{2}\left (\dfrac{-3}{4} \right )\\$
$=\dfrac{3}{8}$

$7. \displaystyle \int_{-1}^{1} \dfrac{2x+3}{x^{2}+3x+7}\: dx$

$I = \displaystyle \int_{-1}^{1} \dfrac{2x+3}{x^{2}+3x+7}\: dx\\$
$Put \: t=x^{2}+3x+7\\$
$dt=2x+3 \: dx\\$

$I = \displaystyle \int_{5}^{11} \dfrac{dt}{t}\\$
$=\bigg[log\left | t \right | \bigg]_{5}^{11}\\$
$=log \: 11-log \: 5\\$
$=log\dfrac{11}{5}$

$8. \displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{1+cos \: x} \: dx$

$I =\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{1+cos \: x} \: dx\\$
$=\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{2cos^{2} \: \frac{x}{2}} \: dx\\$
$=\sqrt{2}\displaystyle \int_{0}^{\frac{\pi}{2}} cos\frac{x}{2} \: dx\\$
$=\sqrt{2}\bigg[\dfrac{sin\frac{x}{2}}{\frac{1}{2}} \bigg]_{0}^{\frac{\pi}{2}}\\$
$=2\sqrt{2} \bigg[sin\dfrac{x}{2} \bigg]_{0}^{\frac{\pi}{2}}\\$
$=2\sqrt{2} \left (sin\frac{\pi}{4}-sin 0 \right )\\$
$=2\sqrt{2} \left (\dfrac{1}{\sqrt{2}}-0 \right )\\$
$=2$

$9. \displaystyle \int_{1}^{2}\dfrac{x-1}{x^{2}} \: dx$

$I =\displaystyle \int_{1}^{2}\dfrac{x-1}{x^{2}}\\$
$=\displaystyle \int_{1}^{2}\left (\dfrac{x}{x^{2}}-\dfrac{1}{x^{2}} \right )\: dx\\$
$=\displaystyle \int_{1}^{2}\left (\dfrac{1}{x}-\dfrac{1}{x^{2}} \right )\: dx\\$
$=\bigg[log \: x-\frac{x^{-1}}{-1} \bigg]_{1}^{2}\\$
$=\bigg[log \: x+\frac{1}{x} \bigg]_{1}^{2}\\$
$=\bigg[log \: 2+\frac{1}{2} \bigg] - \bigg[log \: 1+\frac{1}{1} \bigg]\\$
$=log\: 2+\dfrac{1}{2}- \left (0+1 \right )\\$
$=log\: 2+\dfrac{1}{2}-1\\$
$=log\: 2-\dfrac{1}{2}\\$
$=\dfrac{2 log\: 2-1}{2}\\$
$=\dfrac{1}{2}\left ( 2\: log \: 2-1 \right )$

II. Evaluate the following:

$1. \displaystyle \int_{1}^{4} \: f(x)\: dx \: where f(x)=\left\{\begin{matrix} 4x+3, & 1\leqslant x\leqslant 2\\ 3x+5, & 2< x\leqslant 4 \end{matrix}\right.$

$I= \displaystyle \int_{1}^{4} \: f(x)\: dx\\$
$= \displaystyle \int_{1}^{2} \: f(x)\: dx+ \displaystyle \int_{2}^{4} \: f(x)\: dx\\$
$= \displaystyle \int_{1}^{2} \:\left ( 4x+3 \right ) \: dx+ \displaystyle \int_{2}^{4} \: \left (3x+5 \right ) \: dx\\$
$=\bigg[\dfrac{4x^{2}}{2}+3x \bigg]_{1}^{2}+\bigg[\dfrac{3x^{2}}{2}+5x \bigg]_{2}^{4}\\$
$=\bigg[2x^{2}+3x \bigg]_{1}^{2}+\bigg[\dfrac{3x^{2}}{2}+5x \bigg]_{2}^{4}\\$
$=\bigg[2x^{2}+3x \bigg]_{1}^{2}+\bigg[\dfrac{3x^{2}}{2}+5x \bigg]_{2}^{4}\\$
$=\left (8+6 \right )-\left ( 2+3 \right )+ \left (24+20 \right )- \left (6+10 \right )\\$
$=14-5+44-16\\$
$=58-21\\$
$=37$

$2. \displaystyle \int_{0}^{2} \: f(x)\: dx \: where f(x)=\left\{\begin{matrix} 3-2x-x^{2}, & x\leqslant 1\\ x^{2}+2x-3, & 1< x\leqslant 2 \end{matrix}\right.$

$I= \displaystyle \int_{0}^{2} \: f(x)\: dx\\$
$= \displaystyle \int_{0}^{1} \: f(x)\: dx+ \displaystyle \int_{1}^{2} \: f(x)\: dx\\$
$=I_{1}+I_{2}$
$I_{1}=\displaystyle \int_{0}^{1} \: f(x)\: dx\\$
$=\displaystyle \int_{0}^{1} \: \left (3-2x-x^{2} \right )\: dx\\$
$=\bigg[3x-\dfrac{2x^{2}}{2}-\dfrac{x^{3}}{3} \bigg]_{0}^{1}\\$
$=\left (3-1-\dfrac{1}{3} \right )-\left (0-0-0 \right )\\$
$=\dfrac{9-3-1}{3}\\$
$=\dfrac{5}{3}\\$
$I_{2}=\displaystyle \int_{1}^{2} \: f(x)\: dx\\$
$=\displaystyle \int_{1}^{2} \: \left (x^{2}+2x-3 \right )\: dx\\$
$=\bigg[\dfrac{x^{3}}{3}+\dfrac{2x^{2}}{2}-3x \bigg]_{1}^{2}\\$
$=\bigg[\dfrac{x^{3}}{3}+ {x^{2}}-3x \bigg]_{1}^{2}\\$
$=\bigg[\dfrac{x^{3}}{3}+ {x^{2}}-3x \bigg]_{1}^{2}\\$
$=\left (\dfrac{8}{3}+4-6 \right )-\left (\dfrac{1}{3}+1-3 \right )\\$
$=\dfrac{8+12-18}{3} -\dfrac{1+3-9}{3}\\$
$=\dfrac{2}{3}+\dfrac{5}{3}\\$
$=\dfrac{7}{3}\\$
$I=I_{1}+I_{2}\\$
$=\dfrac{5}{3}+\dfrac{7}{3}\\$
$=\dfrac{12}{3}\\$
$=4$

$3. \displaystyle \int_{-1}^{1} \: f(x)\: dx \: where f(x)=\left\{\begin{matrix} x, & x\geqslant 0\\ -x, & x< 0 \end{matrix}\right.$

$I= \displaystyle \int_{-1}^{1} \: f(x)\: dx\\$
$= \displaystyle \int_{-1}^{0} \: (-x) \: dx+ \displaystyle \int_{0}^{1} \: (x)\: dx\\$
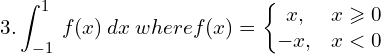
$=\bigg[-\dfrac{x^{2}}{2} \bigg]_{-1}^{0} + \bigg[\dfrac{x^{2}}{2} \bigg]_{0}^{1} \\$
$=\left (3-1-\dfrac{1}{3} \right )-\left (0-0-0 \right )\\$
$=\dfrac{-1}{2} \bigg[x^{2} \bigg]_{-1}^{0} +\dfrac{1}{2} \bigg[x^{2} \bigg]_{0}^{1} \\$
$=\dfrac{-1}{2}\left ( 0-1 \right )+\dfrac{1}{2} (1-0)\\$
$=\dfrac{1}{2}+\dfrac{1}{2}\\$
$=1$

$3. \: f(x)=\left\{\begin{matrix} cx, & 0< x< 1\\ 0, & otherwise \end{matrix}\right.\\$
$Find\: c \: if \: \displaystyle \int_{0}^{1}f(x)=2$

$=\displaystyle \int_{0}^{1}f(x)=2\\$
$=\displaystyle \int_{0}^{1}cx \: dx =2\\$
$=c \displaystyle \int_{0}^{1}x \: dx =2\\$
$=c \left [\dfrac{x^{2}}{2} \right ]_{0}^{1}=2\\$
$=c \left [\dfrac{1}{2}-0 \right ]=2\\$
$=\dfrac{c}{2}=2\\$
$c=4$

If you have any questions on the topic, let us know in the comments section.

Integral Calculus I Exercise 2.8 – 12th Text Book Solutions (Business Maths)

Exercise 2.8

Related Posts:

Leave a Reply Cancel reply

Recent

Exercise 2.8

Related Posts:

Reader Interactions

Leave a Reply Cancel reply

Footer

Recent

Tags