Dear Samacheer Kalvi Students, here are the Integral Calculus II – Exercise 3.1 text book solutions in Business Maths Chapter 3 Integral Calculus II. If you have any doubts, please reach out to us in the comments section.
Click here if you want to revise:
Important Formulas in Integral Calculus II
Text Book Solutions for Integral Calculus I Exercise 3.2
Text Book Solutions for Integral Calculus I Exercise 3.3
Text Book Solutions for Integral Calculus I Exercise 3.4
Exercise 3.1
1. Using Integration, find the area of the region bounded the line 2y + x = 8, the x axis and the lines x = 2, x = 4.
Answer:
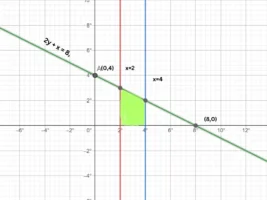
2x+y=8
| x | 0 | 8 |
| y | 4 | 0 |
Since the region lies above the x axis
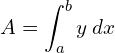
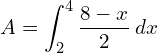
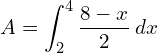
![Rendered by QuickLaTeX.com =\dfrac{1}{2}\bigg [ 8x-\dfrac{x^{2}}{2}\bigg]_{2}^{4}](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-e8e812fe4126efaea24541f16104f3f9_l3.png)
![Rendered by QuickLaTeX.com =\dfrac{1}{2}\bigg [ \left ( 32-8 \right )-\left ( 16-2 \right )\bigg]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-caae7cbb064fc3227e333b27a550fdf6_l3.png)
![]()
![]()
![]()
2. Find the area bounded by the lines y − 2x − 4 = 0, y = 1, y = 3 and the y-axis.
Answer:
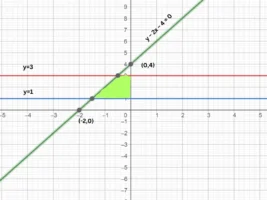
y − 2x − 4 = 0; y= 2x+4
| x | 0 | -2 |
| y | 4 | 0 |
Since the region lies to the left of the y axis
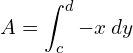
![]()
![]()
![]()
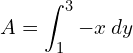
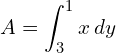
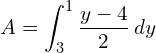
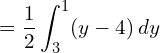
![Rendered by QuickLaTeX.com =\dfrac{1}{2} \bigg[ \dfrac{y^{2}}{2}-4y \bigg]_{3}^{1}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-6905522d625fa7cf7eb8c1e6a665959a_l3.png)
![Rendered by QuickLaTeX.com =\dfrac{1}{2} \bigg[\left( \dfrac{1}{2} -4\right)-\left( \dfrac{9}{2} -12\right)\bigg]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-c5731ebb5778e11e5384de8011d90569_l3.png)
![Rendered by QuickLaTeX.com =\dfrac{1}{2} \left[ \left( -\dfrac{7}{2} \right) - \left( -\dfrac{15}{2} \right) \right]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-63a0abac11492a35f6f9c3451fb2e17b_l3.png)
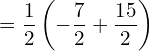
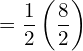
![]()
![]()
![]()
Answer:
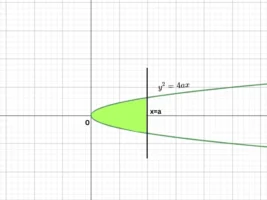
![]()
![]()
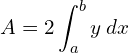
![]()
![]()
![]()
![Rendered by QuickLaTeX.com = 4\: \sqrt{a}\ \left[ \dfrac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1} \right]_{0}^{a}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-a5f43bc7d995b169275fd3a5929ddfa9_l3.png)
![Rendered by QuickLaTeX.com = 4\: \sqrt{a}\ \left[ \dfrac{x^{\frac{3}{2}}}{\frac{3}{2}} \right]_{0}^{a}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-c9ab2c70433dee92f1d89fae24dc65ca_l3.png)
![]()
![]()
![]()
![]()
![]()
4. Find the area bounded by the line y = x, the x-axis and the ordinates x = 1, x = 2.
Answer:
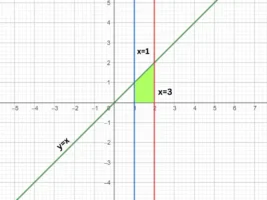
Since the region lies above the x axis,
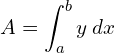
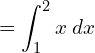
![Rendered by QuickLaTeX.com =\left[ \dfrac{x^{2}}{2} \right]_{1}^{2}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-29aeb8b2df176eb26d0d6cfdf230d9f3_l3.png)
![]()
![]()
5. Using integration, find the area of the region bounded by the line y −1 = x ,the x axis and the ordinates x = –2, x = 3.
Answer:
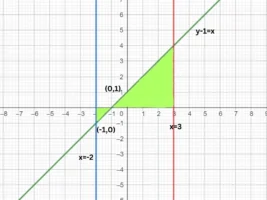
![]()
| x | 0 | -1 |
| y | 1 | 0 |
![]()
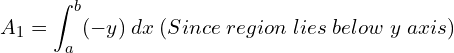
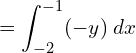
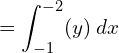
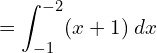
![Rendered by QuickLaTeX.com =\left[ \dfrac{x^{2}}{2}+x \right]_{-1}^{-2}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-d36a312eaa9021b260861499d40b8a26_l3.png)
![]()
![]()
![]()
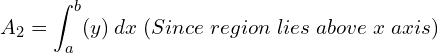
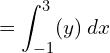
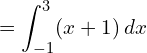
![Rendered by QuickLaTeX.com =\left[ \dfrac{x^{2}}{2}+x \right]_{-1}^{3}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-0f0273098973514ff49dfceba1b90119_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. Find the area of the region lying in the first quadrant bounded by the region y=4x2 ; x=0; y=0; and y=4.
Answer:
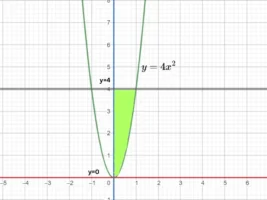
![]()
![]()
![]()
![]()
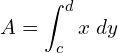
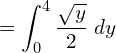
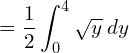
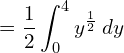
![Rendered by QuickLaTeX.com =\dfrac{1}{2}\left[ \dfrac{ y^{\frac{3}{2}}}{\frac{3}{2}} \right]_{0}^{4}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-35658259cf37b86592f4584ebee49aea_l3.png)
![]()
![]()
![]()
![]()
![]()
Answer:
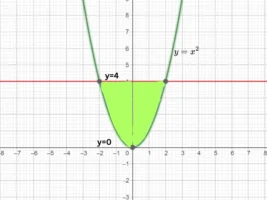
![]()
![]()
![]()
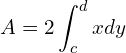
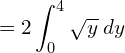
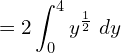
![Rendered by QuickLaTeX.com =2 \left[ \dfrac{y^{\frac{3}{2}}}{\frac{3}{2}} \right]_{0}^{4}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-c7cac09eaaef0f26c1aa1916f87834b1_l3.png)
![]()
![]()
![]()
Leave a Reply