Dear Samacheer Kalvi Students, here are the Integral Calculus II – Exercise 3.2 text book solutions in Business Maths Chapter 3 Integral Calculus II. If you have any doubts, please reach out to us in the comments section.
Click here if you want to revise:
Important Formulas in Integral Calculus II
Text Book Solutions for Integral Calculus I Exercise 3.1
Text Book Solutions for Integral Calculus I Exercise 3.3
Text Book Solutions for Integral Calculus I Exercise 3.4
Exercise 3.2
1. The cost of over haul of an engine is ₹10,000 The operating cost per hour is at the rate of 2x − 240 where the engine has run x km. Find out the total cost if the engine run for 300 hours after overhaul.
Answer:
![]()
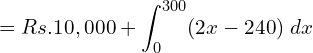
![Rendered by QuickLaTeX.com = Rs.10,000 + \left[ \dfrac{2x^{2}}{2}-240x \right]_{0}^{300}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-5307a1edb2ca661876b6c1b59cb2dbc5_l3.png)
![Rendered by QuickLaTeX.com = Rs.10,000 + \bigg[ x^{2}-240x \bigg]_{0}^{300}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-73c4f5f27ad110c3fe0ce2c9a3a5bb34_l3.png)
![]()
![]()
![]()
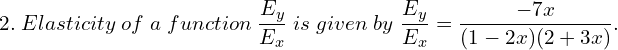
![]()
Answer:

![]()
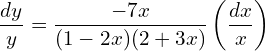
![]()
![]()
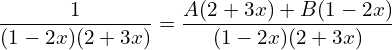
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com log \left| y \right|= - \left[ \dfrac{2 \;log\left| (1-2x) \right|}{-2}+\dfrac{3 \;log\left| (2+3x) \right|}{3} +log \left| c \right|\right]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-8d073aae165b52f11f566f833fd7c2ef_l3.png)
![]()
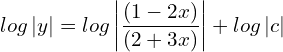


![]()

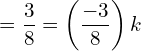
![]()
![]()
![]()
3. The elasticity of demand with respect to price for a commodity is given by (4-x)/x where p is the price when demand is x. Find the demand function when price is 4 and the demand is 2. Also find the revenue function.
Answer:
![]()
![]()
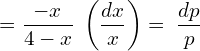
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. A company receives a shipment of 500 scooters every 30 days. From experience it is known that the inventory on hand is related to the number of days x. Since the shipment, I (x) = 500 − 0.03×2 , the daily holding cost per scooter is ₹ 0.3. Determine the total cost for maintaining inventory for 30 days.
Answer:


![Rendered by QuickLaTeX.com =0.3 \bigg[ 500x-\dfrac{0.03x^{3}}{3} \bigg]_{0}^{30}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-1123e31bd294c9777b5f4794344b1b49_l3.png)
![Rendered by QuickLaTeX.com =0.03 \bigg[ 500x-0.01x^{3} \bigg]_{0}^{30}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-4b7b13e01db5c3a8c4695849cdb76546_l3.png)
![]()
![]()
![]()
![]()
5. An account fetches interest at the rate of 5% per annum compounded continuously. An individual deposits ₹1,000 each year in his account. How much will be in the account after 5 years. (e0.25 = 1.284) .
Answer:
![]()

![Rendered by QuickLaTeX.com =1000 \bigg[ \dfrac{e^{0.05t}}{e^{0.05}} \bigg]_{0}^{5}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-4030c3dcc9da3b4c18b4cca8d9d5f476_l3.png)
![]()
![]()
![]()
![]()
![]()
6. The marginal cost function of a product is given by dC/dx = 100 −10x + 0.1x2 where x is the output. Obtain the total and the average cost function of the firm under the assumption, that its fixed cost is ₹ 500.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
7. The marginal cost function is MC = 300x2/5 and fixed cost is zero. Find out the total cost and average cost functions.
Answer:
![]()
![]()
![]()
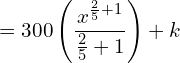
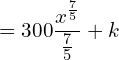
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
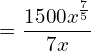
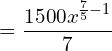
![]()
![]()
![]()
Answer:
![]()
![]()
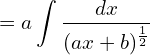
![]()
![Rendered by QuickLaTeX.com = a \left[ \dfrac{(ax+b)^{\frac{-1}{2}+1}}{a\times \dfrac{-1}{2}+1}\right]+k\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-27b46f10293cad761d993d96d2075b10_l3.png)
![]()
![]()
![]()
![]()
![]()
9. Determine the cost of producing 200 air conditioners if the marginal cost (is per unit) is C’ (x) = x2 /200+4 .
Answer:
![]()
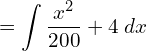
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
10. The marginal revenue (in thousands of Rupees) functions for a particular commodity is 5 + 3e-0.03x where x denotes the number of units sold. Determine the total revenue from the sale of 100 units. (Given e-3 = 0.05 approximately)
Answer:
![]()

![Rendered by QuickLaTeX.com =\bigg[ 5x+\dfrac{3e^{-0.03x}}{-0.03} \bigg]_{0}^{100}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-57095577451331b8c08f77b0e6273660_l3.png)
![Rendered by QuickLaTeX.com =\bigg[5x-\dfrac{e^{-0.03x}}{-0.01} \bigg]_{0}^{100}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-987eba10d324af6bb5358ac88cdac82e_l3.png)
![Rendered by QuickLaTeX.com =\left[ 5(100)-\dfrac{e^{-0.03(100)}}{-0.01} \right]-0-\dfrac{e^{-0}}{.01}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-ff7dd418ad4e85fc8f07f0b1d5371e40_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
11. If the marginal revenue function for a commodity is MR = 9 − 4x2 . Find the demand function.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
12. Given the marginal revenue function 4\(2x+3)2 -1 , show that the average revenue function is P = 4\(6x+9) -1.
Answer:
![]()
![]()
![]()
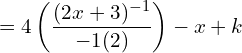
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com =\left[ \dfrac{-2}{(2x+3)x}+\dfrac{2}{3x} \right]-1 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-4832f3801919424a699612f2a2931408_l3.png)
![Rendered by QuickLaTeX.com =\left[ \dfrac{-2 (3)+2(2+3x)}{3x(2x+3)} \right]-1\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-7cf78bf414cfc7b6c298627f7e7fde06_l3.png)
![Rendered by QuickLaTeX.com =\left[ \dfrac{-6+4x+6}{3x(2x+3)} \right]-1\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-24f58d3cef54da12677e7bec8d7d34e6_l3.png)
![]()
![]()
![]()
![]()
13. A firm’s marginal revenue function is MR =20e-x/10 (1-x\10). Find the corresponding demand function.
Answer:
![]()
![]()
![]()
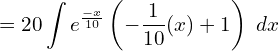
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
14. The marginal cost of production of a firm is given by C'(x) = 5 + 0.13x , the marginal revenue is given by R'(x) = 18 and the fixed cost is ₹ 120. Find the profit function.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
15. If the marginal revenue function is R'(x)= 1500 − 4x − 3x2 . Find the revenue function and average revenue function.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
16. Find the revenue function and the demand function if the marginal revenue for x units is MR= 10 + 3x − x2 .
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
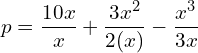
![]()
17. The marginal cost function of a commodity is given by MC= 14000/√7x+4 and the fixed cost is ₹18,000. Find the total cost and average cost.
Answer:
![]()
![]()

![]()
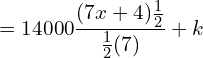
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
18. If the marginal cost (MC) of a production of the company is directly proportional to the number of units (x) produced, then find the total cost function, when the fixed cost is ₹ 5,000 and the cost of producing 50 units is ₹ 5,625.
Answer:
![]()
![]()
![]()
![]()
![]()
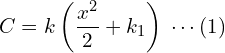
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
19. If MR = 20 − 5x + 3x2 , find total revenue function.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
20. If MR = 14 − 6x + 9x2 , find the demand function.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If you have any doubts or questions, in this chapter, please reach out to us in the comments section.
Leave a Reply