Dear Samacheer Kalvi Students, here are the Integral Calculus II – Exercise 3.3 text book solutions in Business Maths Chapter 3 Integral Calculus II. If you have any doubts, please reach out to us in the comments section.
Click here if you want to revise:
Important Formulas in Integral Calculus II
Text Book Solutions for Integral Calculus I Exercise 3.1
Text Book Solutions for Integral Calculus I Exercise 3.2
Text Book Solutions for Integral Calculus I Exercise 3.4
Exercise 3.3
1. Calculate consumer’s surplus if the demand function p = 50 − 2x and x = 20.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com =\bigg[ 50x-\dfrac{2x^{2}}{2} \bigg]_{0}^{20}-200\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-4fea798a03d79c4df8b8ee864f642e34_l3.png)
![Rendered by QuickLaTeX.com =\bigg[ 50x-x^{2} \bigg]_{0}^{20}-200\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-16dc82644118bb79b87496e970802c0c_l3.png)
![]()
![]()
![]()
2. Calculate consumer’s surplus if the demand function p = 122 − 5x − 2x2 and x = 6.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
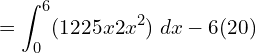
![Rendered by QuickLaTeX.com =\bigg[ 122x-\dfrac{5x^{2}}{2}-\dfrac{2x^{3}}{3} \bigg]_{0}^{ 6}-120\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-e00002afdaeb94d075d6c2b16bb5a967_l3.png)
![Rendered by QuickLaTeX.com =122(6)-\dfrac{5(6)^{2}}{2}-\dfrac{2(6)^{3}}{3} \bigg]_{0}^{ 6}-120\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-b7f5689f51cb1377d2eb83333ee0390d_l3.png)
![]()
![]()
3. The demand function p = 85 − 5x and supply function p = 3x − 35 . Calculate the equilibrium price and quantity demanded. Also calculate consumer’s surplus.
Answer: At equilibrium price, quantity demanded = quantity supplied
Qd =Qs
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
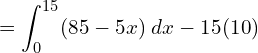
![Rendered by QuickLaTeX.com =\bigg[ 85x-\dfrac{5x^{2}}{2} \bigg]_{0}^{15}-150\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-42461ebd7e90398efdf358b35167d867_l3.png)
![Rendered by QuickLaTeX.com =\bigg[ 85(15)-\dfrac{5(15)^{2}}{2} \bigg]_{0}^{15}-150\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-648991c3d516df9a88cc937e60c9c7df_l3.png)
![]()
![]()
![]()
![]()
![]()
4. The demand function for a commodity is p = e-x .Find the consumer’s surplus when p = 0.5.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![Rendered by QuickLaTeX.com =\bigg[ \dfrac{e^{-x}}{-1} \bigg]_{0}^{log 2}- \left( \dfrac{1}{2} \right)log\;2 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-294b68bdd8660fc498c55e637e121f68_l3.png)
![Rendered by QuickLaTeX.com =-\bigg[ \dfrac{1}{e^{x}} \bigg]_{0}^{log 2}- \left( \dfrac{1}{2} \right)log\;2 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-8ed3ea3e04751bdd668600f7a6fd4ff8_l3.png)
![Rendered by QuickLaTeX.com =- \left[ \dfrac{1}{e^{log\; 2}}-\dfrac{1}{e^{0}} \right]-\left( \dfrac{1}{2} \right)log\;2\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-8f70b6eaf5e600be5e3f5b0553f595b4_l3.png)
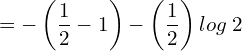
![]()
![]()
5. Calculate the producer’s surplus at x = 5 for the supply function p = 7 + x.
Answer:
![]()
![]()
![]()
![]()
![]()

![Rendered by QuickLaTeX.com =60 \bigg[ 7x+\dfrac{x^{2}}{2} \bigg]_{0}^{5}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-64845251752e090a8635eade2f52ee74_l3.png)
![Rendered by QuickLaTeX.com =60- \left[\left( 7(5)+\dfrac{5^{2}}{2} \right)-(0+0)\right]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-0d0870a2e874927cb542f878db47a700_l3.png)
![]()
![]()
![]()
6. If the supply function for a product is p = 3x + 5x2 .Find the producer’s surplus when x = 4.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
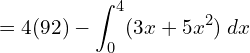
![Rendered by QuickLaTeX.com =368-\bigg[ \dfrac{3x^{2}}{2}+\dfrac{5x^{3}}{3} \bigg]_{0}^{4}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-676154ddce87860a800772ee8cd0d670_l3.png)
![Rendered by QuickLaTeX.com =368- \bigg[ \left( \dfrac{3(4)^{2}}{2}+\dfrac{5(4)^{3}}{3} \right) -\left( 0+0 \right)\bigg]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-bc7869e6a5e73dfa6dde65aad59729b5_l3.png)
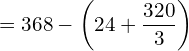
![]()
![]()
![]()
![]()
7. The demand function for a commodity is p = 36/x+4. Find the consumer’s surplus when the prevailing market price is Rs.6.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

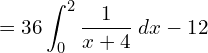
![Rendered by QuickLaTeX.com =36 \; \bigg[ log (x+4) \bigg]_{0}^{2}-12\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-c514d0586609dedddde1fa6a8bb602d6_l3.png)
![]()
![]()
![]()
8. The demand and supply functions under perfect competition are pd= 1600 – x2 and ps = 2x2+ 400 respectively. Find the producer’s surplus.
Answer: At equilibrium price, pd=ps
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
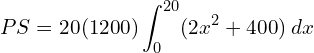
![Rendered by QuickLaTeX.com =24000-\bigg[ \dfrac{2x^{3}}{3}+400x \bigg]_{0}^{20}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-b0dc914b7288f0d953bc417944498fed_l3.png)
![Rendered by QuickLaTeX.com =24000-\bigg[ \left( \dfrac{2(20)^{3}}{3}+400(20) \right) -\left( 0+0 \right)\bigg]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-64aca6cf087b732a353619437ea18a18_l3.png)

![]()
![]()
![]()
![]()
9. Under perfect competition for a commodity the demand and supply laws are pd= 8\x+1and ps = x+3/2 respectively. Find the consumer’s and producer’s surplus.
Answer: At equilibrium price, pd=ps
![]()
![]()

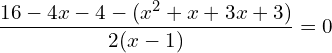


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![Rendered by QuickLaTeX.com =\bigg[ \left( 8\; log (x+1)-2x \right) \bigg]_{0}^{1}-2\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-56ade182932d97b68fbb3a601e89d9b0_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
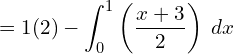

![Rendered by QuickLaTeX.com =2-\dfrac{1}{2} \bigg[ \dfrac{x^{2}}{2}+3x \bigg]_{0}^{1}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-e8c07707b9447e11922cf582999bb2ca_l3.png)
![Rendered by QuickLaTeX.com =2-\dfrac{1}{2} \left[ \left( \dfrac{1}{2}+3 \right)- \left( 0+0 \right) \right]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-76c32d6cc271777ac24ee07554a9c9cc_l3.png)

![]()
![]()
10. The demand equation for a products is x = √100 − p and the supply equation is x = p/2-10. Determine the consumer’s surplus and producer’s surplus, under market equilibrium.
Answer:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
At market equilibrium, pd =ps
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
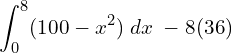
![Rendered by QuickLaTeX.com =\bigg[ 100x-\dfrac{x^{3}}{3} \bigg]_{0}^{8}-288\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-434e16f012d34ac291d173b100c4499a_l3.png)
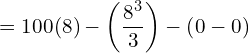
![]()
![]()
![]()
![]()

![Rendered by QuickLaTeX.com =288-\bigg[ \dfrac{2x^{2}}{2}+20x \bigg]_{0}^{8}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-228e56ec61e5f7298ae4b3ea3527c6f4_l3.png)
![Rendered by QuickLaTeX.com =288-\bigg[ \dfrac{2(8)^{2}}{2}+20(8) \bigg]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-7fde9ff787d69bfba3cdb60d4a4a7798_l3.png)
![]()
![]()
![]()
11. Find the consumer’s surplus and producer’s surplus for the demand function pd = 25 − 3x and supply function ps = 5 + 2x.
Answer: At market equilibrium, pd =ps
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![Rendered by QuickLaTeX.com =\bigg[ 25x-\dfrac{3x^{2}}{2} \bigg]_{0}^{4}-52\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-c5fe0930abc20994ab376ef9441dbd48_l3.png)
![Rendered by QuickLaTeX.com =\left[ \left(25(4)- \dfrac{3\times4^{2}}{2} \right) -\left( 0-0 \right) \right]-52\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-6df0c25794ce0c45128e30018e7871ae_l3.png)
![]()
![]()
![]()
![]()

![Rendered by QuickLaTeX.com =52-\bigg[ 5x +\dfrac{2x^{2}}{2}\bigg]_{0}^{4}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-6fe2997da216152b5b7b153eafd17a24_l3.png)
![Rendered by QuickLaTeX.com =52-\bigg[5x+x^{2} \bigg]_{0}^{4}\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-8702ddfd2876bca6aa7417611d3b4ab2_l3.png)
![]()
![]()
![]()
![]()
If you have any doubts in this exercise, please let us know in the comments section.
Leave a Reply