Numerical Methods Text Book Solutions Exercise 5.1

Dear Class 12 Samacheer Kalvi students, here are the Business Maths Chapter 5 Numerical Methods Exercise 5.1 Text Book Solutions for your study.

Exercise 5.1

$1.\; \text{Evaluate} \; \Delta (\log \; ax)$

$\Delta f(x)=f(x+h)-f(x)\\$
$\Delta (log\; ax)= log\;a (x+h)-log (ax)\\$
$=\dfrac{log \;a (x+h)}{ax}\\$
$= \dfrac{log(x+h)}{x}\\$
$=log \left( \dfrac{x}{x}+\dfrac{h}{x} \right)\\$
$=log \left(1 +\dfrac{h}{x} \right)$

$2.\; If\; y = x^{3} - x^{2} + x -1\; calculate\; the \;values\; of \;y \;for\; x = 0,1, \\$
$2,3,4,5 \;and \;form\; the\; forward\;differences\; table.$

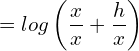
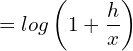
Answer: The equation is:

$y = x^{3} - x^{2} + x -1$

x	0	1	2	3	4	5
y	-1	0	5	20	51	104

x	y	∆y	∆² y	∆³ y	∆⁴ y	∆⁵ y
0	-1
1	0	1
2	5	5	4
3	20	15	10	6
4	51	31	16	6	0
5	104	53	22	6	0	0

$3.\; If \;h = 1 \;then \; prove \;that\; (E^{-1}\Delta)x^{3} = 3x^{2} - 3x +1$

$Given: h= 1\; To \;prove:\; (E^{-1}\Delta)x^{3} = 3x^{2} - 3x +1$

$Proof\\$
$(E^{-1}\Delta)x^{3}= E^{-1}\Delta (x^{3})=E^{-1}(\Delta x^{3})\\$
$=E^{-1}\left( (x+h)^{3}-x^{3} \right)\\$
$=E^{-1} (x+h)^{3}-E^{-1}x^{3})\\$
$=(x+h-h)^{3}-(x-h)^{3}\\$
$=x^{3}-(x-h)^{3}\\$
$At \; h=1\;\\$
$=x^{3}-(x-1)^{3}\\$
$=x^{3}-(x^{3}-3x^{2}+3x-1)\\$
$=x^{3}-x^{3}+3x^{2}-3x+1\\$
$=RHS$

$4.\; If \;f(x) = x^{2}+ 3x \;then \;show \;that\; \Delta f(x)= 2x + 4\\$

$f(x) = x^{2}+ 3x\\$
$\Delta f(x) = f(x+h)-f(x)\\$
$=(x+h)^{2}+3(x+h)-(x^{2}+ 3x)\\$
$At \;h=1\\$
$=(x+1)^{2}+3(x+1)-x^{2}- 3x\\$
$=x^{2}+2x+1+3x+3-x^{2}- 3x\\$
$=2x+4\\$
$=RHS$

$5.\; Evaluate\; \Delta\left[ \dfrac{1}{(x+1)(x+2)} \right]\; by \; taking \; '1'\; as\; the\; interval\; of\; differencing.$

Answer:

$\Delta f(x)= f(x+h)-f(x)\\$
$\dfrac{1}{(x+1)(x+2)} =\dfrac{1}{(x+1+1)(x+2+1)}-\dfrac{1}{(x+1)(x+2)}\\$
$= \left[ \dfrac{1}{(x+2)(x+3)} \right]-\left[ \dfrac{1}{(x+1)(x+2)} \right] \\$
$=\dfrac{x+1-x-3}{(x+1)(x+2)(x+3)}\\$
$=\dfrac{-2}{(x+1)(x+2)(x+3)}$

6. Find the missing entry in the following table.

x	0	1	2	3	4
y_x	1	3	9	–	81

Answer: Since only 4 values are given:

$\Delta ^{4}y_{0}=0\\$
$(E^{-1})^{4}y_{0}=0\\$
$&&&&&&&1&&&&&&\\$
$1 &&&&&&1&&1&&&&&\\$
$2 &&&&&1&&2&&1&&&&\\$
$3 &&&&1&&3&&3&&1&&&\\$
$4 &&&1&&4&&6&&4&&1&&\\$
$(E^{4}-4E^{3}+6E^{2}-4E+1)y_{0}=0\\$
$y_{4}-4y_{3}+6y_{2}-4y_{1}+y_{0}=0\\$
$=81-4y_{3}+6(9)-4(3)+1=0\\$
$=81-4y_{3}+54-12+1=0\\$
$=124-4y_{3}=0\\$
$-4y_{3}=-124\\$
$y_{3}=\dfrac{-124}{-4}\\$
$y_{3}=31$

7. Following are the population of a district.

Year(x)	1881	1891	1901	1911	1921	1931
Population (y) in Thousands	363	391	421	–	467	501

Find the population of the year 1911.

Answer: Since only 5 values are given:

$\Delta ^{5}y_{0}=0\\$
$(E^{-1})^{5}y_{0}=0\\$
$\begin{array}{c} 1 \\ 1 \quad 1 \\ 1 \quad 2 \quad 1 \\ 1 \quad 3 \quad 3 \quad 1 \\ 1 \quad 4 \quad 6 \quad 4 \quad 1 \\ 1 \quad 5 \quad 10 \quad 10 \quad 5 \quad 1 \\ \end{array} \\$
$(E^{5}-5E^{4}+10E^{3}-10E^{2}+5E+1)y_{0}=0\\$
$(y_{5}-5y_{4}+10y_{3}-10y_{2}+5y_{1}-y_{0}=0\\$
$(501-5(467)+10y_{3}-10(421)+5(391)-363=0\\$
$(501-2335+10y_{3}-4210+1955-363=0\\$
$(2456-6908+10y_{3}=0\\$
$(-4452+10y_{3}=0\\$
$10y_{3}=4452\\$
$10y_{3}=4452\\$
$y_{3}= \dfrac{4452}{10}\\$
$y_{3}= 445.2\\$

Since the population is in thousands, population for the year 1991 = 445.2 x 1000= 4,45,200.

8. Find the missing entries from the following.

x	0	1	2	3	4	5
y=f(x)	0	–	8	15	–	35

Answer: Since only 4 values of f(x) are given:

$\Delta ^{4}y_{0}=0\\$
$(E^{-1})^{4}y_{0}=0\\$
$\begin{array}{c} 1 \\ 1 \quad 1 \\ 1 \quad 2 \quad 1 \\ 1 \quad 3 \quad 3 \quad 1 \\ 1 \quad 4 \quad 6 \quad 4 \quad 1 \\ \end{array} \\$
$(E^{4}-4E^{3}+6E^{2}-4E+1)y_{0}=0\\$
$y_{4}-4y_{3}+6y_{2}-4y_{1}+y_{0}=0\\$
$y_{4}-4(15)+6(8)-4y_{1}+0=0\\$
$y_{4}-60+48-4y_{1}+0=0\\$
$y_{4}-12-4y_{1}=0\\$
$y_{4}-4y_{1}=12\; \cdots (1)\\$
$Let \; \Delta ^{4}y_{1}=0\\$
$(E^{-1})^{4}y_{1}=0\\$
$(E^{4}-4E^{3}+6E^{2}-4E+1)y_{1}=0\\$
$y_{5}-4y_{4}+6y_{3}-4y_{2}+y_{1}=0\\$
$35-4y_{4}+6(15)-4(8)+y_{1}=0\\$
$35-4y_{4}+90-32+y_{1}=0\\$
$93-4y_{4}+y_{1}=0\\$
$-4y_{4}+y_{1}=-93\; \cdots (2)\\$
$Multiply \; Eq. (1)\; by \;4 \\$
$-4y_{4}+y_{1} =-93\\$
$4y_{4}-16y_{1} =48$
$\noindent\rule{3 cm}{0.5pt}\\$
$-15y_{1}=-45\\$
$y_{1}=\dfrac{-45}{-15}\\$
$y_{1}=3\\$
$Substituting\; y_{1}=3\; in (2) \\$
$-4y_{4}+3=-93 \cdots (2)\\$
$-4y_{4} = -96\\$
$y_{4} =\dfrac{-96}{-4}\\$
$y_{4} =24$