Dear Class 12 Samacheer Kalvi students, here are the Business Maths Chapter 5 Numerical Methods Exercise 5.2 Text Book Solutions for your study.
Numerical Methods Exercise 5.2 Text Book Solutions
1. Using graphic method, find the value of y when x = 48 from the following data:
| x | 40 | 50 | 60 | 70 |
| y | 6.2 | 7.2 | 9.1 | 12 |
Answer: Plot the points (40,6.2), (50,7.2), (60,9.1) and (70,12)
Scale: x axis: 1 cm = 10 units; y axis: 1 cm = 1 unit;
2. The following data relates to indirect labour expenses and the level of output.
| Months | Jan | Feb | Mar | Apr | May | Jun |
| Units of output | 200 | 300 | 400 | 640 | 540 | 580 |
| Indirect labour expenses (Rs.) | 2500 | 2800 | 3100 | 3820 | 3220 | 3640 |
Estimate the expenses at a level of output of 350 units, by using graphic method.
Answer: Plot the points (200,2500), (300,2800), (400,3100), (640, 3820), (540, 3220), (580,3640)
From the graph, when x=350, y=2900.
Expenses of 350 units = Rs. 2900
Scale: x axis: 1 cm = 100 units; y axis: 1 cm = 500 units
3. Using Newton’s forward interpolation formula find the cubic polynomial.
| x | 0 | 1 | 2 | 3 |
| f(x) | 1 | 2 | 1 | 10 |
Answer: Newton’s forward interpolation formula
![]()
![]()
![]()
![]()
![]()
The difference table is:
| x | y | ∆y | ∆2 y | ∆3 y |
| 0 | 1 | |||
| 1 | 2 | 1 | ||
| 2 | 1 | -1 | -2 | |
| 3 | 10 | 9 | 10 | 12 |
![]()
![]()
![]()
![]()
![]()
4. The population of a city in a censes taken once in 10 years is given below. Estimate the population in the year 1955.
| Year | 1951 | 1961 | 1971 | 1981 |
| Population in lakhs | 35 | 42 | 58 | 84 |
![]()
![]()
![]()
![]()
![]()
Since 1955 lies between 1951 and 1961, we can use Newton’s forward interpolation formula.
![]()
The difference table is:
| x | y | ∆y | ∆2 y | ∆3 y |
| 1951 | 35 | |||
| 1961 | 42 | 7 | ||
| 1971 | 58 | 16 | 9 | |
| 1981 | 84 | 26 | 10 | 1 |
![]()
![]()
![]()
![]()
5. In an examination the number of candidates who secured marks between certain interval were as follows:
| Marks | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 |
| No of candidates | 41 | 62 | 65 | 50 | 17 |
Estimate the number of candidates whose marks are less than 70.
| Marks | No of candidates | Cumulative frequency |
| -.5-19.5 | 41 | 41 |
| 19.5-39.5 | 62 | 103 |
| 39.5-59.5 | 65 | 168 |
| 59.5-79.5 | 50 | 218 |
| 79.5-99.5 | 17 | 235 |
| x | y | ∇y | ∇2 y | ∇3 y | ∇4 y |
| Less than 19.5 | 41 | ||||
| Less than 39.5 | 103 | 62 | |||
| Less than 59.5 | 168 | 65 | 3 | ||
| Less than 79.5 | 218 | 50 | -15 | -18 | |
| Less than 99.5 | 235 | 17 | -33 | -18 | 0 |
Since we need the number of candidates whose marks are less than 70, we can use Newton’s backward interpolation formula.
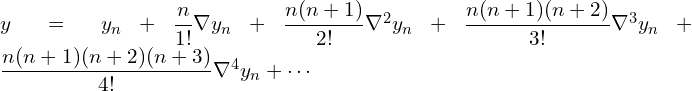
![]()
![]()
![]()
![]()
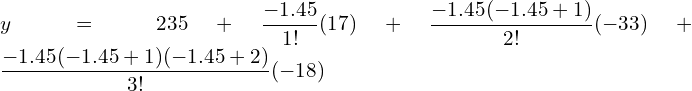
![]()
![]()
![]()
![]()
![]()
6. Find the value of f (x) when x = 32 from the following table:
| x | 30 | 35 | 40 | 45 | 50 |
| f(x) | 15.9 | 14.9 | 14.1 | 13.3 | 12.5 |
Since x=32 lies between 30 and 35, we can use Newton’s forward interpolation formula.
| x | y | ∆y | ∆2 y | ∆3 y | ∆4 y |
| 30 | 15.9 | ||||
| 35 | 14.9 | -1 | |||
| 40 | 14.1 | -0.8 | 0.2 | ||
| 45 | 13.3 | -0.8 | 0 | -0.2 | |
| 50 | 12.5 | -0.8 | 0 | 0 | 0.2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
7. The following data gives the melting point of a alloy of lead and zinc where ‘t’ is the temperature in degree c and P is the percentage of lead in the alloy.
| P | 40 | 50 | 60 | 70 | 80 | 90 |
| T | 180 | 204 | 226 | 250 | 276 | 304 |
Find the melting point of the alloy containing 84 percent lead.
Since x=84 lies between 80 and 90, we can use Newton’s backward interpolation formula.
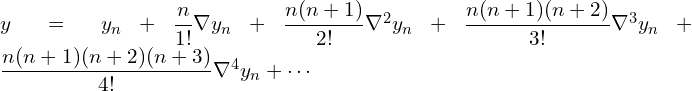
| x | y | ∇y | ∇2 y | ∇3 y | ∇4 y | ∇4 y |
| 40 | 180 | |||||
| 50 | 204 | 24 | ||||
| 60 | 226 | 22 | -2 | |||
| 70 | 250 | 24 | 2 | 4 | ||
| 80 | 276 | 26 | 2 | 0 | -4 | |
| 90 | 304 | 28 | 2 | 0 | 0 | 4 |
![]()
![]()
![]()
![]()
![]()
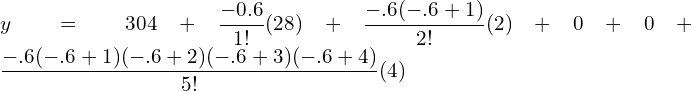
![]()
![]()
8. Find f (2.8) from the following table:
| x | 0 | 1 | 2 | 3 |
| f(x) | 1 | 2 | 11 | 34 |
Since 2.8 lies between 2 and 3, we can use Newton’s backward interpolation formula.
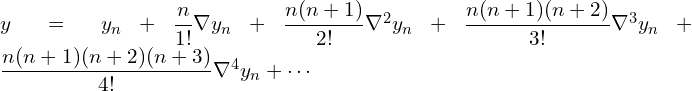
![]()
![]()
![]()
![]()
| x | y | ∇y | ∇2 y | ∇3 y |
| 0 | 1 | |||
| 1 | 2 | 1 | ||
| 2 | 11 | 9 | 8 | |
| 3 | 34 | 23 | 14 | 6 |
![]()
![]()
![]()
![]()
9. Using interpolation estimate the output of a factory in 1986 from the following data.
| Year | 1974 | 1978 | 1982 | 1990 |
| Output in 1000 tonnes | 25 | 60 | 80 | 170 |
Answer: Since the intervals are unequal, we can use LaGrange’s formula.
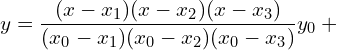
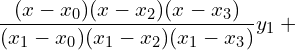
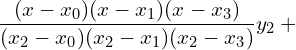
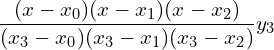
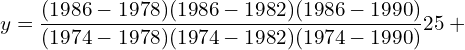
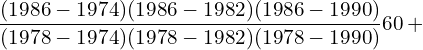
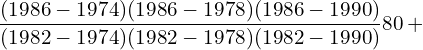
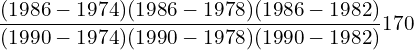
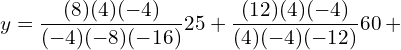
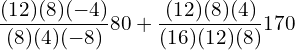
![]()
![]()
10. Use Lagrange’s formula and estimate from the following data the number of workers getting income not exceeding Rs. 26 per month.
| Income not exceeding(Rs.) | 15 | 25 | 30 | 35 |
| No. of workers | 36 | 40 | 45 | 48 |
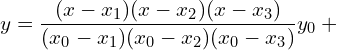
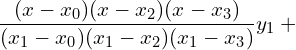
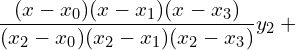
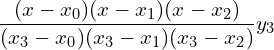
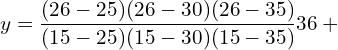
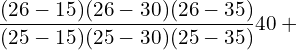
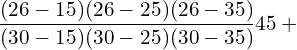
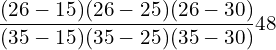
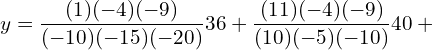
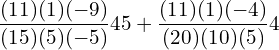
![]()
![]()
![]()
11. Using interpolation estimate the business done in 1985 from the following data.
| Year | 1982 | 1983 | 1984 | 1986 |
| Business done (in lakhs) | 150 | 235 | 365 | 525 |
Answer: Since the intervals are unequal, we can use LaGrange’s formula.
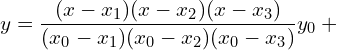
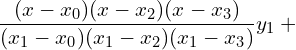
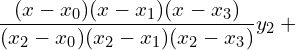
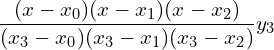
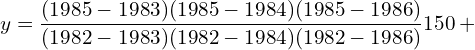
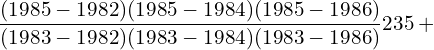
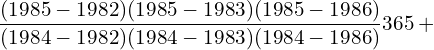
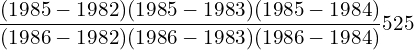
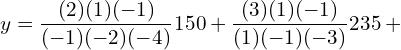
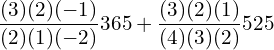
![]()
![]()
12. Using interpolation, find the value of f(x) when x = 15
| x | 3 | 7 | 11 | 19 |
| f(x) | 42 | 43 | 47 | 60 |
Answer: Since the intervals are unequal, we can use LaGrange’s formula.
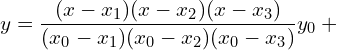
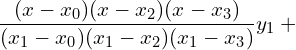
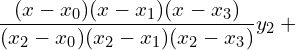
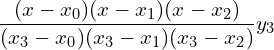
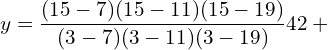
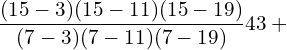
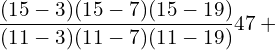
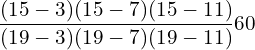
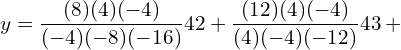
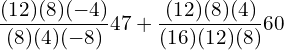
![]()
![]()
Leave a Reply