Dear Class 12 Samacheer Kalvi students, here are the Text Book Solutions for Exercise 6.1 Business Maths Chapter 6 Random Variable and Mathematical for your reference and study.
You can find links to the other exercises below.
Important Formulas in Random Variable and Mathematical Expectation
Text Book Solutions for Differential Equations Exercise 6.2
Text Book Solutions for Differential Equations Exercise 6.3
Exercise 6.1
![]()
| X | 0 | 1 | 2 | 3 |
| P(X=x) | 0.3 | 0.2 | 0.4 | 0.1 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| X | 0 | 1 | 2 | 3 |
| P(X=x) | 0.3 | 0.5 | 0.9 | 1 |
![]()

![]()
| X | 3 | 5 | 8 | 10 |
| P(x) | 0.3 | 0.2 | 0.3 | 0.2 |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| X | 3 | 5 | 8 | 10 |
| P(x) | 0.3 | 0.5 | 0.8 | 1 |
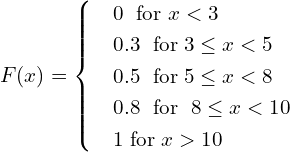
Graph of F(x)
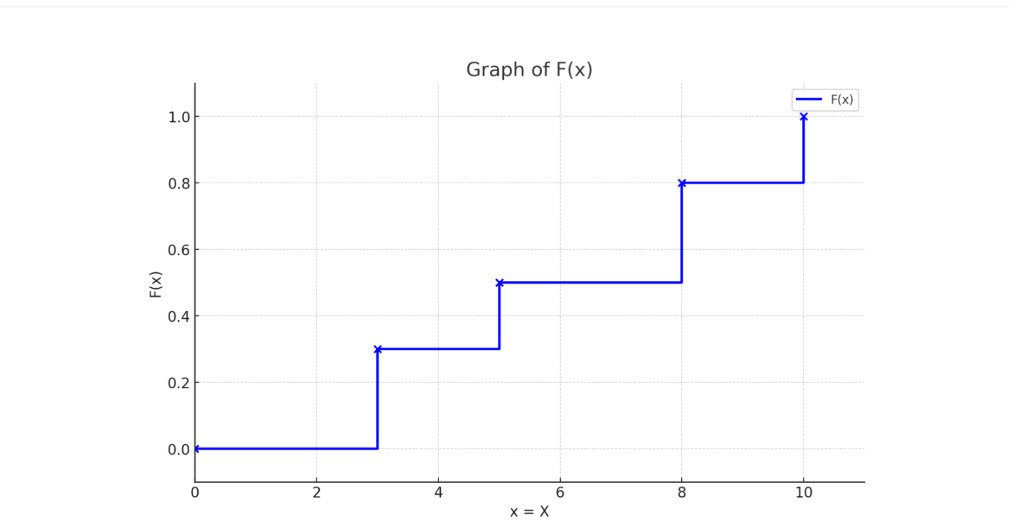
![]()
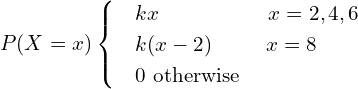
![]()
| X | 2 | 4 | 6 | 8 |
| P(x) | 2k | 4k | 6k | 6k |
Since p(x) is p.m.f
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| X | 1 | 2 | 3 | 4 |
| P(x) | k | 2k | 3k | 4k |
![]()
Since p(x) is p.m.f
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| X | 0 | 1 | 2 |
| P(x) | 1/4 | 1/2 | 1/4 |
![]()
| Value of X=x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p(x) | 0 | k | 2k | 2k | 3k | k2 | 2k2 | 7k2 +k |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
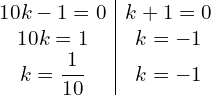
![]()
![]()
![]()
![]()
![]()
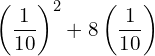
![]()
![]()
![]()
![]()
![]()
![]()
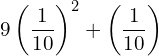
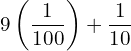
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
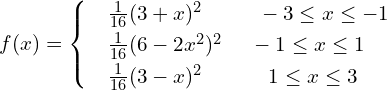
![]()
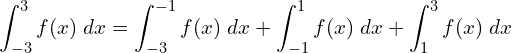
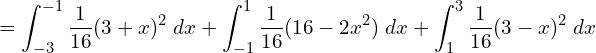
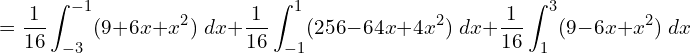
![]()
![Rendered by QuickLaTeX.com =\displaystyle \frac{1}{16} \Bigg[(-9-6+1)-(9-18+9)+ (256-64+4)-(256+64+4) +(9-18+9)-(9-6+1) \Bigg]\\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-096e230f86c93ff6b0bef6767fe52fd5_l3.png)
![]()
![]()
![]()
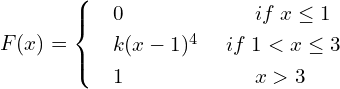
![]()
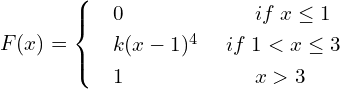
![]()
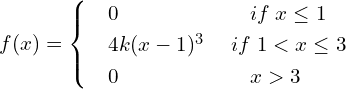
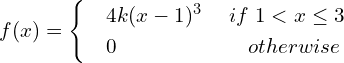
![]()
![]()

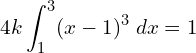
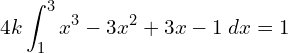
![Rendered by QuickLaTeX.com 4k\bigg[\frac{x^{4}}{4}-\frac{3x^{3}}{3}+\frac{3x^{2}}{2}-x\bigg]_{1}^{3}=1 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-73e751777c03a2ef39e014c1d233d4f0_l3.png)
![Rendered by QuickLaTeX.com 4k\bigg[\left( \frac{81}{4}-27+\frac{27}{2}-3 \right)- \bigg(\frac{1}{4}-1+\frac{3}{2}-1 \bigg)\bigg ] =1 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-40e885fda5eea6d39a1db77b19efd59d_l3.png)
![Rendered by QuickLaTeX.com 4k\bigg[\left( \frac{81}{4}+\frac{27}{2}-30 \right)- \bigg(\frac{1}{4}+\frac{3}{2}-2 \bigg)\bigg ] =1 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-d4d62b2aac5a93054668bec6532725f8_l3.png)
![Rendered by QuickLaTeX.com 4k\bigg[\left( \frac{81+54-120}{4} \right)- \bigg(\frac{1+6-8}{4} \bigg)\bigg ] =1 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-ce37ebca5d3001845efb25215c801127_l3.png)
![Rendered by QuickLaTeX.com 4k\bigg[\left( \frac{15}{4} \right)- \bigg(\frac{-1}{4} \bigg)\bigg ] =1 4k\bigg[\frac{16}{4}\bigg ] =1 \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-16ee55a32b3885c591ea0afd722a3fa3_l3.png)
![]()
![]()
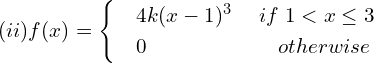
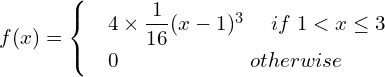
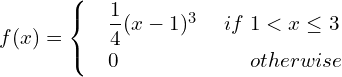
![]()
![]()
![]()
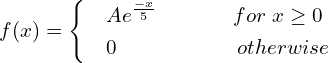
![]()
![]()
![]()
![]()
![]()
![]()
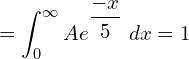
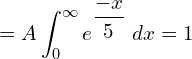
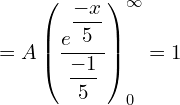
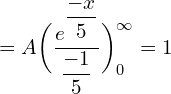
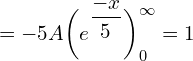
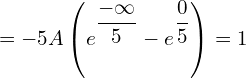
![]()
![]()
![]()
![]()
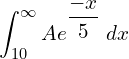
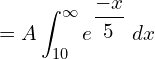
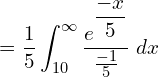
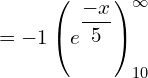
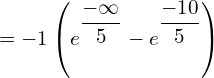
![]()
![]()
![]()
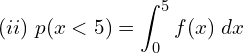
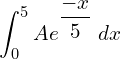
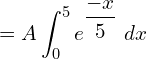
![Rendered by QuickLaTeX.com =\dfrac{1}{5}\left[ \frac{e^{\dfrac{-x}{5}}}{\frac{-1}{5}} \right]_{0}^{5} \\](https://mightyguru.in/wp-content/ql-cache/quicklatex.com-8dad70512816f4ad92e791c1cafaca04_l3.png)
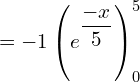
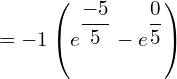
![]()
![]()
![]()
![]()
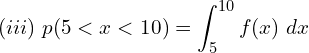
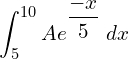
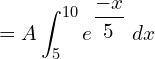
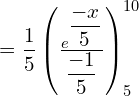
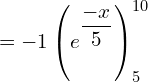
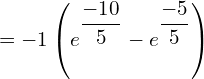
![]()
![]()
![]()
![]()
![]()
![]()
![]()
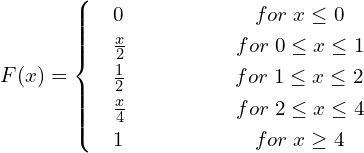
![]()
![]()
![]()
![]()
![]()
![]()
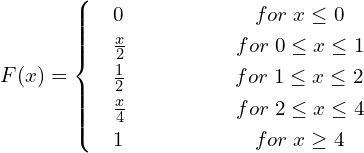
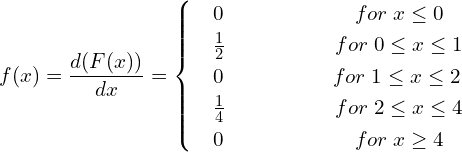

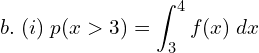
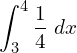
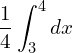
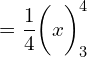
![]()
![]()
![]()
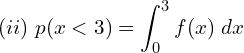
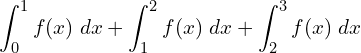
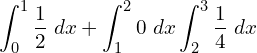
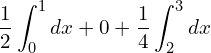
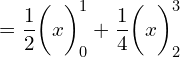
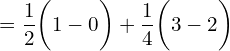
![]()
![]()
![]()
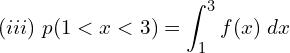
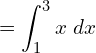
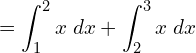
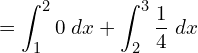
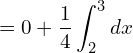
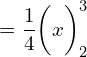
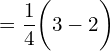
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| Basis of Difference | Discrete Random Variable | Continuous Random Variable |
| Definition | Takes only specific, countable values. | Takes any value within a given range or interval. |
| Number of Possible Values | Finite or countably infinite (e.g., 0, 1, 2, 3, …). | Uncountably infinite — values can take any point on a continuum. |
| Examples | Number of students in a class, number of cars in a parking lot, number of heads in coin tosses. | Height of students, time taken to complete a task, temperature of a city. |
| Type of Data | Count data (quantitative but discrete). | Measurement data (quantitative and continuous). |
| Probability Distribution | Represented by a probability mass function (PMF). | Represented by a probability density function (PDF). |
| Probability of a Specific Value | P(X=x) can be greater than 0. | P(X=x)=0 for any specific value; probabilities are found over intervals. |
| Graph Representation | Bar graph (individual bars for each value). | Smooth curve (continuous line over a range). |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The Probability Mass Function (PMF) represents the probability that a discrete random variable takes on a specific value. It assigns a probability to each possible outcome and satisfies two main conditions:
- (i) p(x) ≥ 0, for all x
- (ii) and the sum of all probabilities equals one, i.e., ∑p(x)=1.
The PMF is used only for discrete random variables such as the number of heads in coin tosses or the number of students present in a class. Graphically, a PMF is shown as a bar graph with distinct, separated points.
The Probability Density Function (PDF), applies to continuous random variables. It describes how probabilities are distributed over a range of values rather than specific points. The PDF, denoted by f(x), must satisfy two conditions:
(i) f(x) ≥ 0 for all x; and
(ii) the total area under the curve equals one.
The graph of a PDF is a smooth curve, such as the familiar bell-shaped normal distribution.
Probability Distribution Function, also known as the Cumulative Distribution Function (CDF), gives the probability that a random variable X takes a value less than or equal to a specified number x. For discrete variables, the CDF is obtained by summing probabilities from the PMF up to x. For continuous variables, it is found by integrating the PDF from negative infinity to x. Graphically, it appears as a step function for discrete variables or a smooth, continuously increasing curve for continuous variables.
![]() \text{(ii) W continuous random variable? } \\[/latex]
\text{(ii) W continuous random variable? } \\[/latex]
A discrete random variable is one that can take only specific, countable values, such as 0, 1, 2, 3, and so on. The main properties of a discrete random variable are:
- It assumes a finite or countably infinite set of values.
- The probability of each possible value is given by its Probability Mass Function (PMF), denoted by p(x)=P(X=x)
- The probability of any value is non-negative, i.e., p(x)≥0 for all x.
- The sum of all probabilities equals one: ∑p(x)=1.
- The cumulative distribution function (CDF), F(x)=P( X ≤ x), increases in steps as x increases.
A continuous random variable, in contrast, can take any value within a given range or interval. Its main properties are:
- It assumes an uncountably infinite number of possible values within a continuum.
- The probability is described by a Probability Density Function (PDF), denoted by f(x), which satisfies f(x)≥0 and
 .
. - The probability of the variable taking any exact value is always zero, Probabilities are instead determined over intervals:

- The Cumulative Distribution Function (CDF),
 is a continuous and non-decreasing function that ranges from 0 to 1.
is a continuous and non-decreasing function that ranges from 0 to 1. - The graph of a continuous random variable is typically a smooth curve, such as a normal or exponential distribution.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
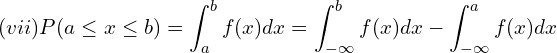
![]()
![]()
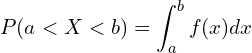
Leave a Reply